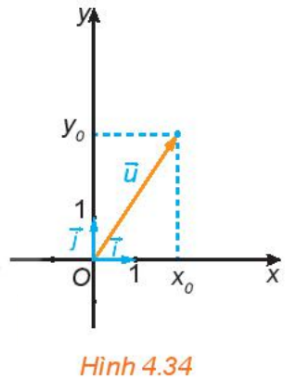
Lý thuyết Vecto trong mặt phẳng tọa độ - SGK Toán 10 Kết nối tri thức

1. TỌA ĐỘ CỦA MỘT VECTO

+) Trên mặt phẳng, hệ trục gồm hai trục Ox, Oy vuông góc với nhau tại O được gọi là hệ trục tọa độ.

Mặt phẳng chứa hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy hay mặt phẳng Oxy.

+) Vecto đơn vị là vecto hướng là chiều dương, có độ dài bằng 1.

Quy ước: vecto đơn vị của trục Ox là $\overrightarrow i$, vecto đơn vị của trục Oy là $\overrightarrow j$.
Điểm O gọi là gốc tọa độ, trục Ox gọi là trục hoành, trục Oy gọi là trục tung.

+) Với mỗi vecto $\overrightarrow u$ trên mặt phẳng Oxy, có duy nhất cặp số $({x_0};{y_0})$ sao cho $\overrightarrow u  = {x_0}.\overrightarrow i  + {y_0}.\overrightarrow j$

Ta nói vecto $\overrightarrow u$ có tọa độ $({x_0};{y_0})$ và viết $\overrightarrow u  = ({x_0};{y_0})$ hoặc $\overrightarrow u ({x_0};{y_0})$.

Các số ${x_0},{y_0}$ tương ứng được gọi là hoành độ, tung độ của $\overrightarrow u$.

+) Hai vecto bằng nhau khi và chỉ khi chúng có cùng tọa độ

$\overrightarrow u (x;y) = \overrightarrow v (x';y') \Leftrightarrow \left\{ \begin{array}{l}x = x'\\y = y'\end{array} \right.$

2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO

+) Cho hai vecto $\overrightarrow u  = (x;y)$ và $\overrightarrow v  = (x';y')$. Khi đó:

$\begin{array}{l}\overrightarrow u  + \overrightarrow v  = (x + x';y + y')\\\overrightarrow u  - \overrightarrow v  = (x - x';y - y')\\k\overrightarrow u  = (kx;ky)\quad (k \in \mathbb{R})\end{array}$

+) Vecto $\overrightarrow v \;(x';y')$ cùng phương với vecto $\overrightarrow u \;(x;y) \ne \overrightarrow 0$

$\Leftrightarrow \exists \;k \in \mathbb{R}:x' = kx,\;y' = ky$ hay $\frac{{x'}}{x} = \frac{{y'}}{y}$ nếu $xy \ne 0.$

+) Điểm M có tọa độ $(x;y)$ thì vecto $\overrightarrow {OM}$ có tọa độ $(x;y)$ và độ dài $\left| {\overrightarrow {OM} } \right| = \sqrt {{x^2} + {y^2}}$

+) Với hai điểm $M(x;y)$ và $N(x';y')$ thì $\overrightarrow {MN}  = (x' - x;y' - y)$

Khoảng cách giữa hai điểm M, N là $MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{(x' - x)}^2} + {{(y' - y)}^2}}$

+) Trung điểm M của đoạn thẳng AB có tọa độ là $\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)$

+) Trọng tâm G của tam giác ABC có tọa độ là $\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)$