Lý thuyết về một số hệ thức về cạnh và góc trong tam giác vuôngTrong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại. 1.Một số hệ thức về cạnh và góc trong tam giác vuông 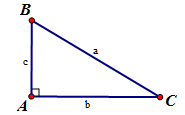 Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Ta có : \(b = a.\sin B = a.\cos C\); \(c = a.\sin C = a.\cos B;\) \(b = c.\tan B = c.\cot C\); \(c = b.\tan C = b.\cot B.\) Trong một tam giác vuông +) Cạnh góc vuông $=$ (cạnh huyền ) $\times $ (sin góc đối) $=$ (cạnh huyền ) $\times $ (cosin góc kề) +) Cạnh góc vuông $=$ (cạnh góc vuông còn lại ) $\times $ (tan góc đối) $=$ (cạnh góc vuông còn lại ) $\times $ (cot góc kề). Chú ý Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại. 2. Các dạng toán thường gặp Dạng 1: Giải tam giác vuông Phương pháp: + Giải tam giác là tính độ dài các cạnh và số đo các góc dựa vào dữ kiện cho trước của bài toán. + Trong tam giác vuông, ta dùng hệ thức giữa cạnh và các góc của một tam giác vuông để tính toán. + Các bài toán về giải tam giác vuông bao gồm : Bài toán 1: Giải tam giác vuông khi biết độ dài một cạnh và số đo một góc nhọn. Bài toán 2: Giải tam giác vuông khi biết độ dài hai cạnh. Dạng 2: Tính cạnh và góc của tam giác Phương pháp: Bằng cách kẻ thêm đường cao ta làm xuất hiện tam giác vuông để áp dụng các hệ thức giữa cạnh và góc thích hợp.
|














