Lý thuyết về hàm số

I. Các kiến thức cần nhớ

1. Định nghĩa hàm số

Nếu đại lượng $y$  phụ thuộc vào đại lượng thay đổi $x$  sao cho với mỗi giá trị của $x$  ta luôn xác định được chỉ một giá trị tương ứng của $y$ thì $y$ được gọi là hàm số của $x$ và $x$ gọi là biến số.

Nhận xét: Nếu đại lượng $y$ là hàm số của đại lượng $x$  thì mỗi giá trị của đại lượng $x$ đều có một giá trị tương ứng duy nhất của đại lượng $y$ ( hay mỗi giá trị của $x$ không thể có hơn một giá trị tương ứng của đại lượng $y$).

Chú ý:

+ Khi $x$  thay đổi mà $y$  luôn nhận một giá trị thì $y$ được gọi là hàm hằng.

+ Hàm số có thể được cho bằng bảng, bằng công thức,…

+ Khi $y$ là hàm số của $x$  ta có thể viết: $y = f\left( x \right);y = g\left( x \right);...$

2. Mặt phẳng tọa độ

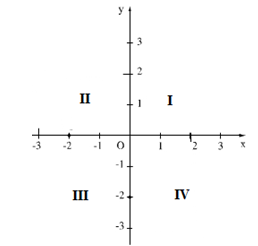* Tọa độ một điểm:

Trên mặt phẳng tọa độ:

+ Mỗi điểm $M$  xác định một cặp số $\left( {{x_0};{y_0}} \right).$ Ngược lại mỗi cặp số $\left( {{x_0};{y_0}} \right)$ xác định một điểm $M$ .

+ Cặp số $\left( {{x_0};{y_0}} \right)$ gọi là tọa độ của điểm $M$ , ${x_0}$ là hoành độ, ${y_0}$ là tung độ của điểm $M.$

+ Điểm $M$có tọa độ $\left( {{x_0};{y_0}} \right)$ kí hiệu là $M\left( {{x_0};{y_0}} \right).$

II. Các dạng toán thường gặp

Dạng 1: Tìm giá trị của hàm số tại giá trị cho trước của biến số

Phương pháp:

+ Nếu hàm số được cho bằng bảng, ta tìm trong bảng giá trị của hàm số tương ứng với giá trị cho trước của biến số.

+ Nếu hàm số được cho bằng công thức, ta thay giá trị đã cho của biến vào công thức và tính giá trị tương ứng của hàm số.

Dạng 2: Viết công thức xác định hàm số

Phương pháp:

Căn cứ vào sự tương quan giữa các đại lượng để lập công thức

Dạng 3: Viết tọa độ của điểm cho trước trên mặt phẳng tọa độ

Phương pháp:

+ Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.

+ Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.

+ Hoành độ và tung độ tìm được là tọa độ của điểm đã cho

Dạng 4: Biểu diễn các điểm có tọa độ cho trước trên mặt phẳng tọa độ

Phương pháp:

+ Từ điểm biểu diễn hoành độ của điểm cho trước kẻ đường thẳng song song với trục tung

+ Từ điểm biểu diễn tung độ của điểm cho trước kẻ đường thẳng song song với trục hoành

+ Giao điểm của hai đường thẳng  vừa dựng là điểm phải tìm.