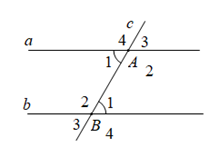
Lý thuyết về các góc tạo bởi một đường thẳng cắt hai đường thẳngNếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì... 1. Góc so le trong, góc đồng vị
Trên hình vẽ ta có: - Hai cặp góc so le trong: \(\widehat{A_{1}}\) và \(\widehat{B_{3}}\); \(\widehat{A_{4}}\) và \(\widehat{B_{2}}\) - Bốn cặp góc đồng vị: \(\widehat{A_{1}}\) và \(\widehat{B_{1}}\); \(\widehat{A_{2}}\) và \(\widehat{B_{2}}\) \(\widehat{A_{3}}\) và \(\widehat{B_{3}}\); \(\widehat{A_{4}}\) và \(\widehat{B_{4}}\). 2. Tính chất Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\), trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: a) Hai góc so le trong còn lại bằng nhau. b) Hai góc đồng vị (trong mỗi cặp) bằng nhau. c) Hai góc trong cùng phía bù nhau Ví dụ: Đường thẳng c cắt hai đường thẳng song song a và b (như hình vẽ). \({\widehat A_1} = {\widehat B_1} \Rightarrow \left\{ \begin{array}{l}{\widehat A_2} = {\widehat B_2}\\{\widehat A_3} = {\widehat B_1}\\{\widehat A_2} + {\widehat B_1} = {180^0}\end{array} \right.\) HocTot.Nam.Name.Vn
|