Lý thuyết trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh(c.c.c)Tính chất: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. 1. Các kiến thức cần nhớ  Nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau theo trường hợp cạnh-cạnh-cạnh. Ví dụ: AB=A′B′BC=B′C′AC=A′C′}⇒ΔABC=ΔA′B′C′(c.c.c) 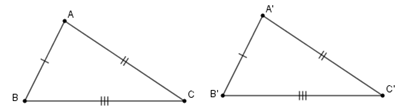 2. Các dạng toán thường gặp Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh-cạnh. Phương pháp: Sử dụng trường hợp bằng nhau thứ nhất của tam giác: “Nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.” Dạng 2: Sử dụng trường hợp bằng nhau cạnh-cạnh-cạnh để chứng minh các cạnh góc bằng nhau, tính số đo góc. Phương pháp: + Xác định hai tam giác có các góc cần chứng minh bằng nhau hoặc cần tính số đo. + Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh-cạnh. + Suy ra hai góc tương ứng bằng nhau hoặc số đo góc cần tính.  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
