Lý thuyết số phứcSố phức z = a + bi có phần thực là a, phần ảo là b - Số phức z=a+bi có phần thực là a, phần ảo là b (a,b∈R và i2=−1) - Số phức bằng nhau a+bi=c+di⇔a=c và b=d - Số phức z=a+bi được biểu diễn bởi điểm M(a;b) trên mặt phẳng toạ độ. - Độ dài của →OM là môđun của số phức z, kí hiệu là |z|=→OM=√a2+b2 - Số phức liên hợp của z=a+bi và ¯z=a−bi. Chú ý - Mỗi số thực là số phức có phần ảo bằng 0. Ta có R⊂C. - Số phức bi (b∈R) là số thuần ảo (phần thực bằng 0) - Số i được gọi là đơn vị ảo. - Số phức viết dưới dạng z=a+bi (a,b∈R), gọi là dạng đại số của số phức. - Ta có: |¯z|=|z| z=¯z⇔z là số thực. z=−¯z⇔z là số ảo. 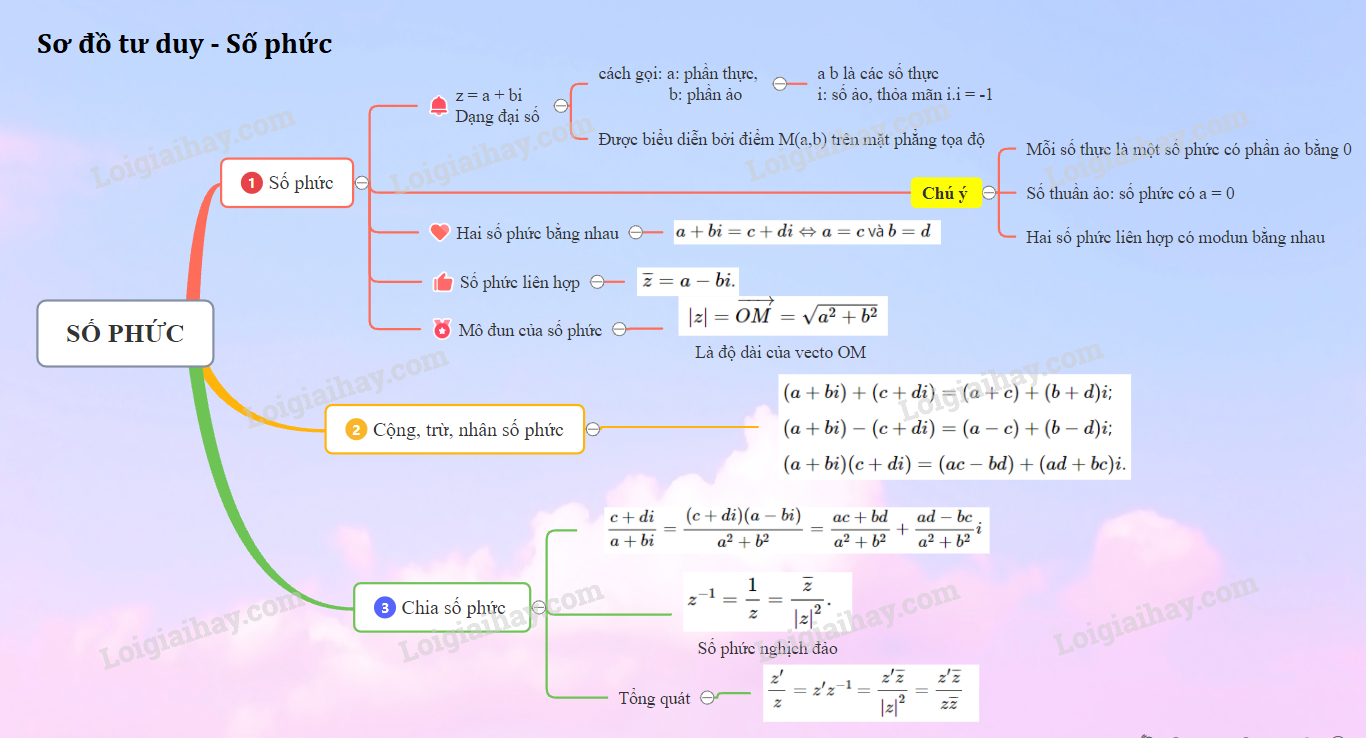  HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
