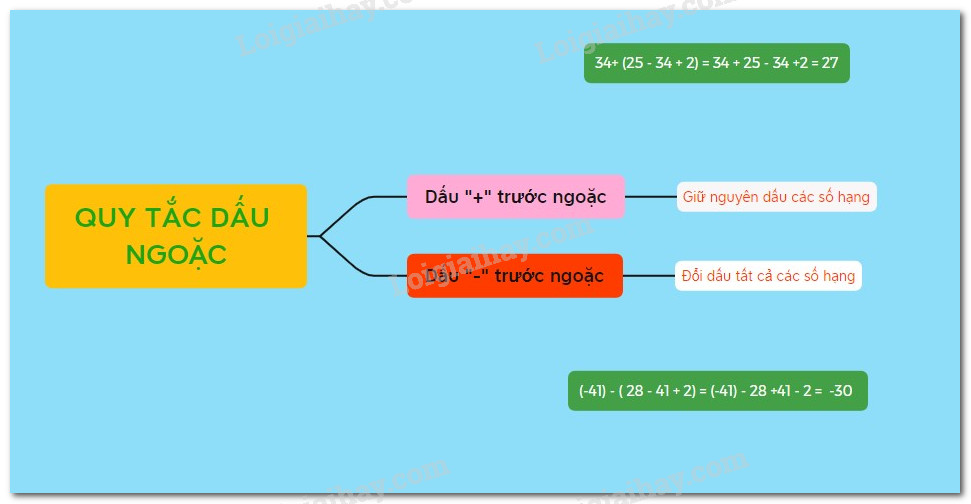
Lý thuyết Quy tắc dấu ngoặc Toán 6 KNTT với cuộc sốngLý thuyết Quy tắc dấu ngoặc Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... 1. Phép trừ hai số nguyên Muốn trừ số nguyên \(a\) cho số nguyên \(b\), ta cộng \(a\) với số đối của b: \(a - b = a + \left( { - b} \right)\) Nhận xét: Phép trừ trong \(\mathbb{N}\) không phải bao giờ cũng thực hiện được, còn phép trừ trong \(\mathbb{Z}\) luôn thực hiện được. Chú ý: Cho hai số nguyên \(a\) và \(b\). Ta gọi \(a - b\) là hiệu của \(a\) và \(b\) (\(a\) được gọi là số bị trừ, \(b\) là số trừ). Ví dụ 1: a) \(6 - 9 = 6 + \left( { - 9} \right) = - \left( {9 - 6} \right) = - 3\). b) \(8 - \left( { - 4} \right) = 8 + 4 = 12\). c) \( - 8 - \left( { - 9} \right) = - 8 + 9 = 9 - 8 = 1\). Ví dụ 2: Nhiệt độ trong phòng ướp lạnh đang là \({3^o}C\), bác Nhung vặn nút điều chỉnh giảm \({4^O}C\).Nhiệt độ phòng sau khi giảm là bao nhiêu độ. Giải Do bác Nhung giảm nhiệt độ đi \({4^o}C\), nên ta làm phép trừ: \(3 - 4 = 3 + \left( { - 4} \right) = - \left( {4 - 3} \right) = - 1\). Vậy nhiệt độ phòng ướp lạnh sau khi giảm là \( - {1^o}C\). 2. Quy tắc dấu ngoặcKhi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc: - Có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc \( + \left( {a + b - c} \right) = a + b - c\) - Có dấu “-”, thì phải đổi dấu tất cả các số hạng trong ngoặc \( - \left( {a + b - c} \right) = - a - b + c\) Chú ý: Trong một biểu thức, ta có thể: + Thay đổi tùy ý vị trí của các số hạng kèm theo dấu của chúng. \(a - b - c = - b + a - c = - c - b + a.\) + Đặt dấu ngoặc để nhóm các số hạng một cách tùy ý. Nếu trước dấu ngoặc là dấu “-” thì phải đổi dấu tất cả các số hạng trong ngoặc. \(a - b - c = \left( {a - b} \right) - c = a - \left( {b + c} \right).\) Ví dụ 1: \(\begin{array}{l}673 + \left[ {2021 - \left( {2021 + 673} \right)} \right] = 673 + \left[ {2021 - 2021 - 673} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 673 + \left( { - 673} \right) = 0\end{array}\) Ví dụ 2: \(\begin{array}{l}12 + 13 + 14 - 15 - 16 - 17 = \left( {12 - 15} \right) + \left( {13 - 16} \right) + \left( {14 - 17} \right)\\ = \left( { - 3} \right) + \left( { - 3} \right) + \left( { - 3} \right) = - \left( {3 + 3 + 3} \right) = - 9\end{array}\).
|