Lý thuyết Phương trình đường thẳng - SGK Toán 10 Kết nối tri thức

A. Lý thuyết

1. Phương trình tổng quát của đường thẳng

a) Vecto pháp tuyến của đường thẳng

Nhận xét:

- Nếu $\overrightarrow n$ là một vecto pháp tuyến của $\Delta$ thì $k\overrightarrow n$ $(k \ne 0)$ cũng là một vecto pháp tuyến của $\Delta$.

- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto pháp tuyến của đường thẳng đó.

b) Phương trình tổng quát của đường thẳng

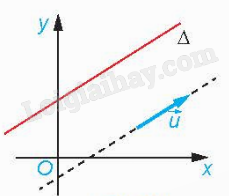
2. Phương trình tham số của đường thẳng

a) Vecto chỉ phương của đường thẳng

Nhận xét:

- Nếu $\overrightarrow u$ là một vecto chỉ phương của $\Delta$ thì $k\overrightarrow u$ $(k \ne 0)$ cũng là một vecto chỉ phương của $\Delta$.

- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto chỉ phương của đường thẳng đó.

b) Phương trình tham số của đường thẳng

B. Bài tập

Lập phương trình đường thẳng $\Delta$ thỏa mãn:

a) Đi qua M(-2;-3) và có $\overrightarrow n  = (2;5)$ là vecto pháp tuyến.

b) Đi qua M(3;-5) và có $\overrightarrow u  = (2; - 4)$ là vecto chỉ phương.

c) Đi qua A(-3;4) và B(1;-1).

Giải:

a) Phương trình $\Delta$ là $2(x + 2) + 5(y + 3) = 0 \Leftrightarrow 2x + 5y + 19 = 0$.

b) Phương trình $\Delta$ là $\frac{{x - 3}}{2} = \frac{{y + 5}}{{ - 4}} \Leftrightarrow 4x + 2y - 2 = 0 \Leftrightarrow 2x + y - 1 = 0$.

c) Phương trình $\Delta$ là $\frac{{x + 3}}{{1 - ( - 3)}} = \frac{{y - 4}}{{ - 1 - 4}} \Leftrightarrow \frac{{x + 3}}{4} = \frac{{y - 4}}{{ - 5}} \Leftrightarrow 5x + 4y - 1 = 0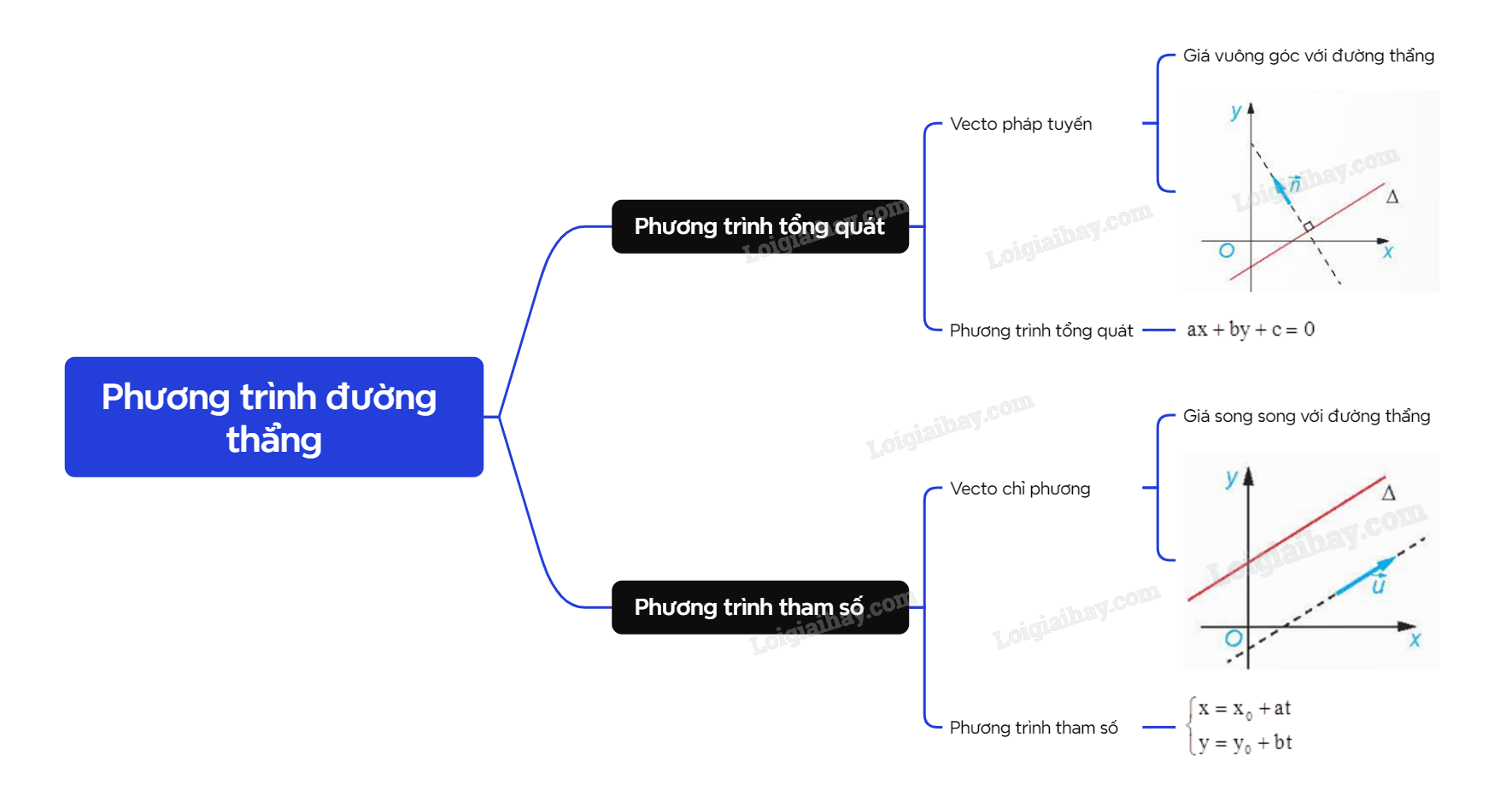$.