Lý thuyết Phép cộng các số nguyên Toán 6 Cánh diềuLý thuyết Phép cộng các số nguyên Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu Tổng hợp đề thi học kì 2 lớp 6 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Phép cộng số nguyên I. Cộng hai số nguyên cùng dấu1. Phép cộng hai số nguyên dương Cộng hai số nguyên dương chính là cộng hai số tự nhiên khác 00. Ví dụ: 2+4=62+4=6. 2. Phép cộng hai số nguyên âm Để cộng hai số nguyên âm, ta làm như sau: Bước 1: Bỏ dấu “-” trước mỗi số Bước 2: Tính tổng của hai số nguyên dương nhận được ở Bước 1. Bước 3: Thêm dấu “-” trước kết quả nhận được ở Bước 2, ta có tổng cần tìm. Nhận xét: - Tổng của hai số nguyên dương là số nguyên dương. - Tổng của hai số nguyên âm là số nguyên âm. Chú ý: Cho a,ba,b là hai số nguyên dương, ta có: (+a)+(+b)=a+b(−a)+(−b)=−(a+b) Ví dụ: (−3)+(−5)=−(3+5)=−8. (−13)+(−7)=−(13+7)=−20. II. Cộng hai số nguyên khác dấuĐể cộng hai số nguyên khác dấu, ta làm như sau: Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại. Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn. Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm. Nhận xét: Hai số nguyên đối nhau có tổng bằng 0: a+(−a)=0. Chú ý: - Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương. - Nếu số dương bằng số đối của số âm thì ta có tổng bằng 0. - Nếu số dương bé hơn số đối của số âm thì ta có tổng âm. Ví dụ: a) (−8)+2=−(8−2)=−6. b) 17+(−5)=17−5=12. c) (−5)+5=0 (Do −5 và 5 là hai số đối nhau). III. Tính chất của phép cộng các số nguyênPhép cộng số nguyên có các tính chất: - Giao hoán: a+b=b+a; - Kết hợp: (a+b)+c=a+(b+c); - Cộng với số 0: a+0=0+a; - Cộng với số đối: a+(−a)=(−a)+a=0. Ví dụ 1: Tính một cách hợp lí: (−34)+(−15)+34 Ta có: (−34)+(−15)+34 =(−15)+(−34)+34 (Tính chất giao hoán) =(−15)+[(−34)+34] (Tính chất kết hợp) =(−16)+0 (cộng với số đối) =−16 (cộng với số 0). Ví dụ 2: Trong một ngày, nhiệt độ ở Mát-xcơ-va lúc 5 giờ là −7oC, đến 10 giờ tăng thêm 6oC và lúc 12 giờ tăng thêm 4oC. Nhiệt độ ở Mát-xcơ-va lúc 12 giờ là bao nhiêu? Giải Nhiệt độ ở Mát-xcơ-va lúc 12 giờ là: (−7)+6+4=(−7)+(6+4)=(−7)+10=10−7=3(oC). 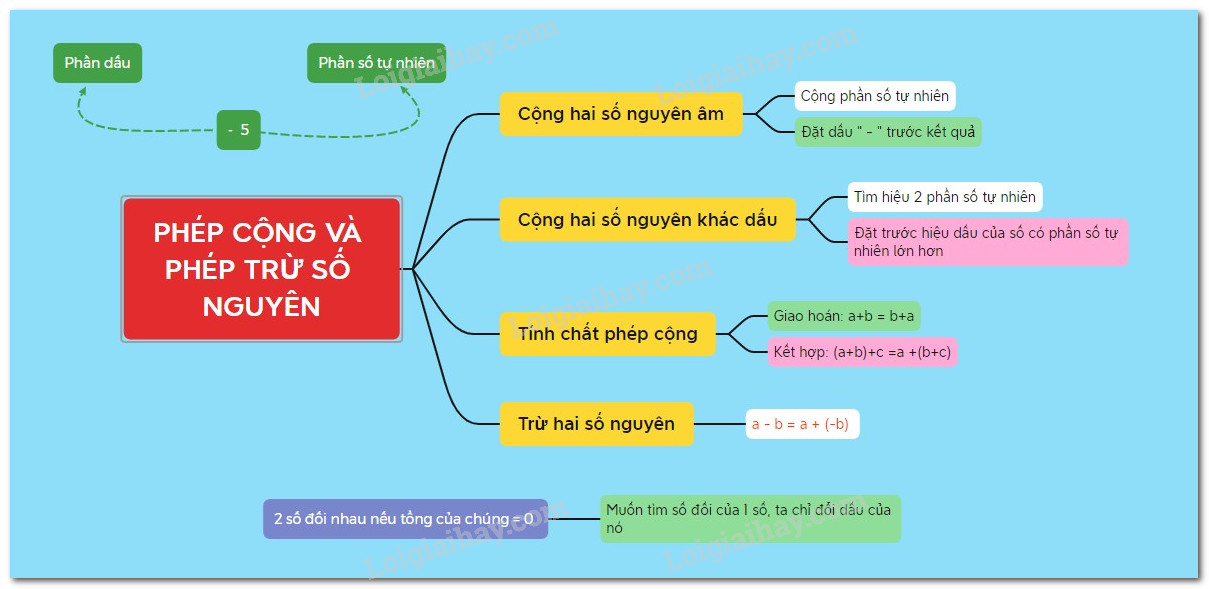
|



















