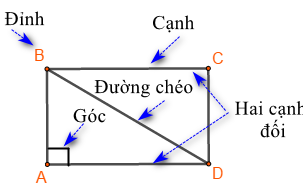
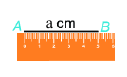
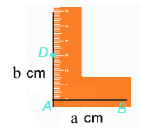
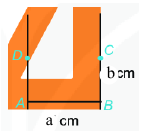
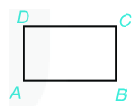
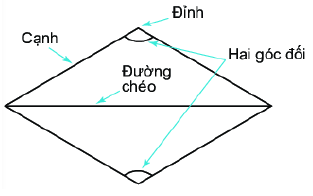
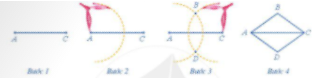
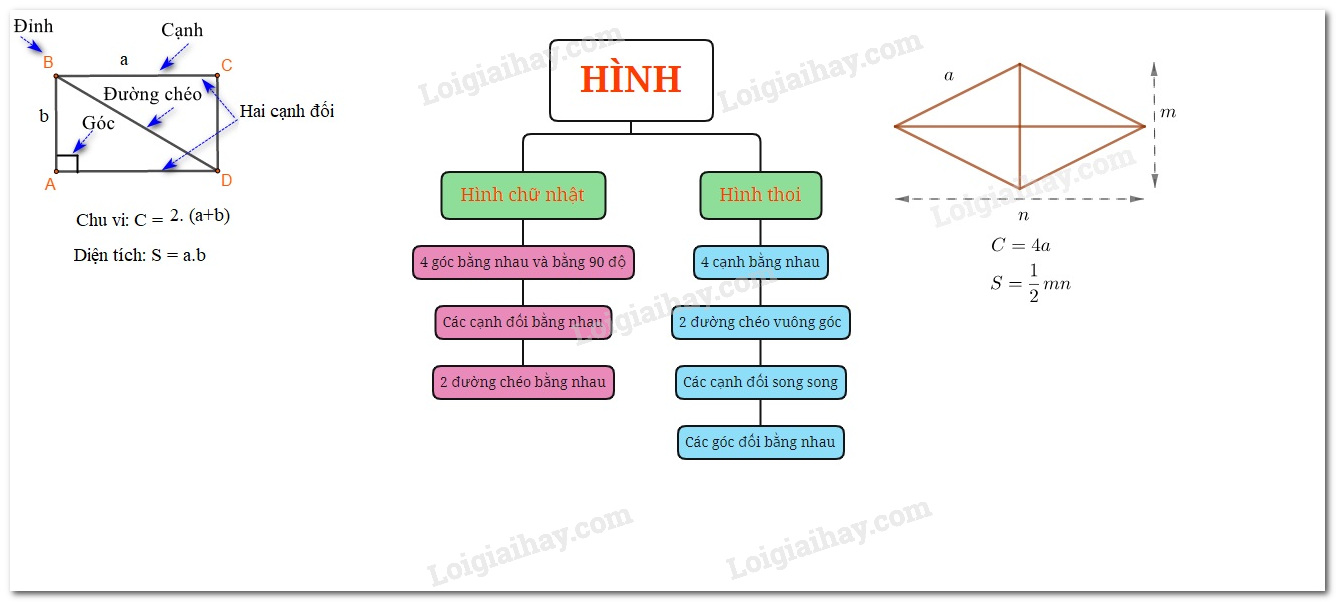
Lý thuyết Hình chữ nhật. Hình thoi Toán 6 Cánh diều

1. Hình chữ nhật

Một số yếu tố cơ bản của hình chữ nhật

- Bốn góc bằng nhau và bằng ${90^0}$

- Các cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

Ví dụ: 

Hình chữ nhật $ABCD$ có:

- Bốn đỉnh A, B, C, D

- Hai cặp cạnh đối diện bằng nhau: $AB = CD;\,\,BC = AD$.

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.

- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:

$AC = BD$ và $OA = OC;\,\,OB = OD$.

Cách vẽ hình chữ nhật có hai cạnh là a và b:

Bước 1: Vẽ đoạn thẳng $AB = a\left( {cm} \right)$

Bước 2: Vẽ đường thẳng vuông góc với $AB$ tại $A$. Trên đường thẳng đó, lấy điểm $D$ sao cho $AD = b\left( {cm} \right)$

Bước 3: Vẽ đường thẳng vuông góc với $AB$ tại $B$. Trên đường thẳng đó, lấy điểm $C$ sao cho $BC = b\left( {cm} \right)$

Bước 4: Nối $C$ và $D$ ta được hình chữ nhật ABCD.

Chu vi và diện tích hình chữ nhật

Hình chữ nhật có độ dài 2 cạnh là a,b thì

Chu vi là: C=2(a+b)

Diện tích là: S=a.b

2. Hình thoi

Một số yếu tố cơ bản của hình thoi

- Bốn cạnh bằng nhau

- Hai đường chéo vuông góc với nhau.

- Các cạnh đối song song với nhau

- Các góc đối bằng nhau

Cách vẽ hình thoi có cạnh là a:

Bước 1: Dùng thước vẽ đoạn thẳng AC

Bước 2: Dùng compa vẽ một phần đường tròn tâm A bán kính AB

Bước 3: Dùng compa vẽ một phần đường tròn tâm C bán kính AB; phần đường tròn này cắt phần đường tròn owrt bước 2 tại 2 điểm B, D

Bước 4: Dùng thước vẽ các đoạn thẳng AB,BC,CD,DA

Chu vi và diện tích của hình thoi

Hình thoi có độ dài cạnh là a, 2 đường chéo là m,n thì

Chu vi là: C=4.a

Diện  tích là: S=$\frac{1}{2}. m.n$