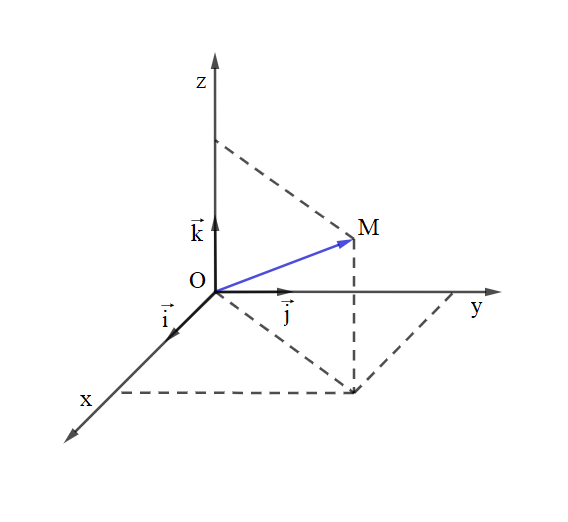
Lý thuyết hệ tọa độ trong không gian

1. Hệ tọa độ trong không gian

Trong không gian cho ba trục tọa độ chung gốc \(O\), đôi một vuông góc với nhau \(x'Ox ; y'Oy ; z'Oz\). Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Đề-các vuông góc \(Oxyz\); \(O\) là gốc tọa tọa độ. Giả sử \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\) lần lượt là các vectơ đơn vị trên các trục \(x'Ox, y'Oy, z'Oz\) (h. 52)

Với điểm \(M\) thuộc không gian \(Oxyz\) thì tồn tại duy nhất bộ số \((x ; y ; z)\) để

\(\overrightarrow{OM}= x.\overrightarrow{i}+y.\overrightarrow{j}+z.\overrightarrow{k}\),

bộ \((x ; y ; z)\) được gọi là tọa độ của điểm \(M(x ; y ; z)\).

Trong không gian Oxyz cho vectơ \(\overrightarrow{a}\), khi đó \(\overrightarrow{a}= a_{1}\overrightarrow{i}+a_{2}\overrightarrow{j}+a_{3}\overrightarrow{k}\)

Ta viết \(\overrightarrow{a}\)\(({a_1};{a_2};{a_3})\) và nói \(\overrightarrow{a}\) có tọa độ \(({a_1};{a_2};{a_3})\) .

2. Biểu thức tọa độ của các phép toán vectơ

Giả sử \(\overrightarrow{a}\)= \(({a_1};{a_2};{a_3})\) và \(\overrightarrow{b}\) = \(({b_1};{b_2};{b_3})\), thì:

\(\overrightarrow{a}+\overrightarrow{b}\) \(= ({a_{1\;}} + {b_1};{a_2}\; + {\rm{ }}{b_2};{\rm{ }}{a_3} + {b_3}\;).\)

\(\overrightarrow{a} - \overrightarrow{b}\) \( = ({a_{1\;}} - {b_1};{a_2}\; - {\rm{ }}{b_2};{\rm{ }}{a_3} - {b_3}\;).\)

\( k.\overrightarrow{a}\) \( = (k{a_1};k{a_2};k{a_3}).\)

3. Tích vô hướng

Cho \(\overrightarrow{a}\)\(({a_1};{a_2};{a_3})\) và \(\overrightarrow{b}\) \(({b_1};{b_2};{b_3})\) thì tích vô hướng \(\overrightarrow{a}\).\(\overrightarrow{b}\) \( = \;{a_1}.{b_1}\; + {\rm{ }}{a_2}.{b_2}\; + {\rm{ }}{a_3}.{b_3}\)

Ta có: \(|\overrightarrow{a}|=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}.\)

Đặt \(\varphi =\left (\widehat{\overrightarrow{a},\overrightarrow{b}} \right )\) , 0 ≤ \(\varphi\) ≤ 180⁰  thì \(cos\varphi =\dfrac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} }{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}\) (với \(\overrightarrow{a}\) ≠ \(\overrightarrow{0}\), \(\overrightarrow{b}\)≠ \(\overrightarrow{0}\))

4. Phương trình mặt cầu

Trong không gian \(Oxyz\), mặt cầu \((S)\) tâm \(I(a ; b ; c)\) bán kính \(R\) có phương trình chính tắc \[{\left( {x - a} \right)^{2\;}} + {\left( {y-b} \right)^2} + {\left( {z-c} \right)^2}\; = {R^2}\]

Mặt cầu có phương trình tổng quát \({x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0\) có tâm \(I\left( { - a; - b; - c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \)