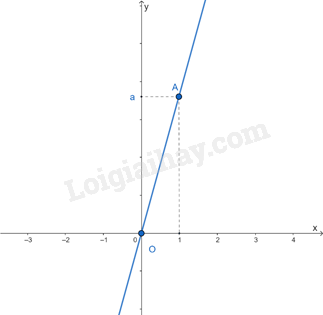
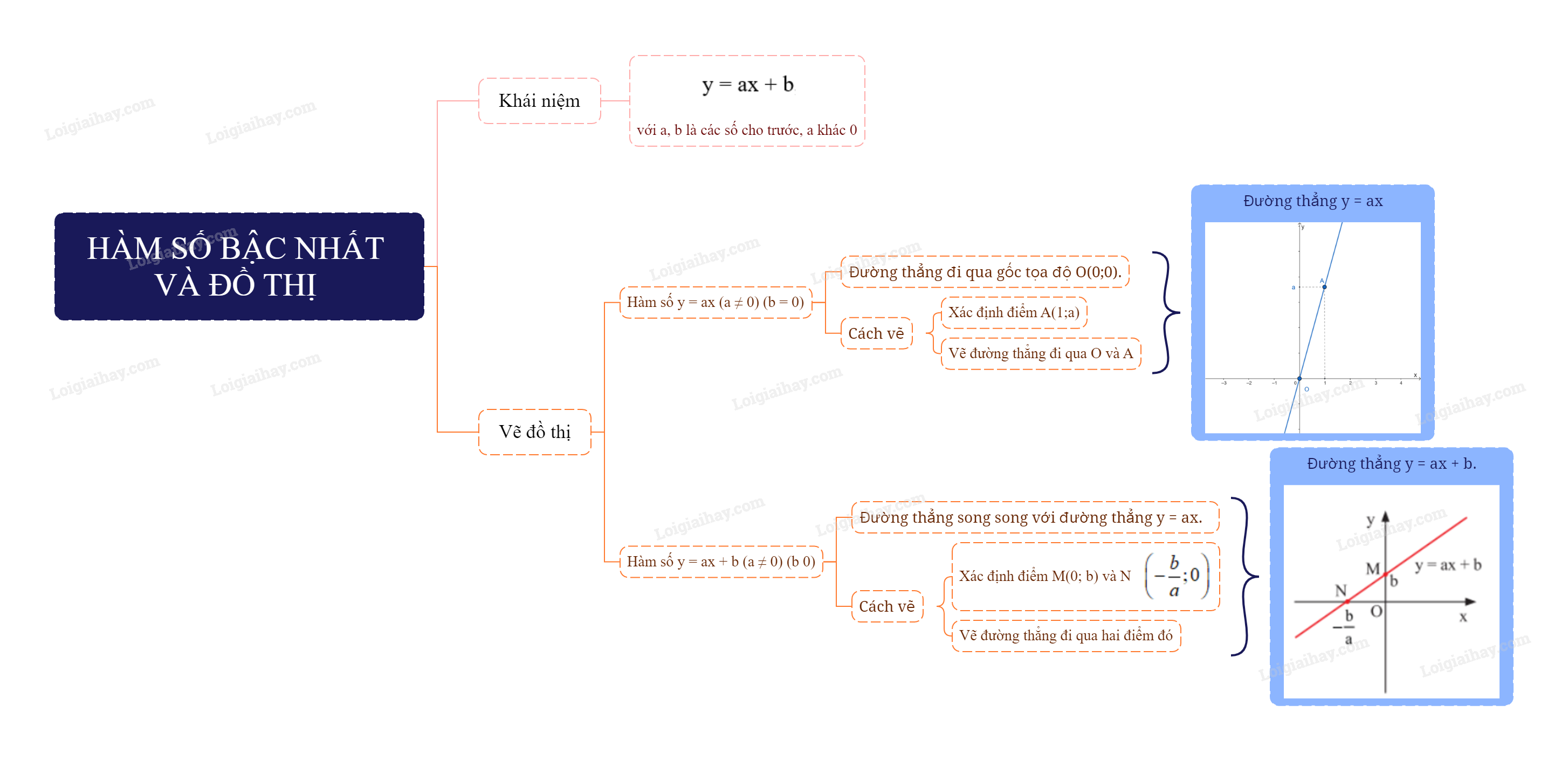
Lý thuyết Hàm số bậc nhất và đồ thị SGK Toán 8 - Cùng khám pháHàm số bậc nhất là gì? 1. Định nghĩa Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b với a, b là các số cho trước và a khác 0. Ví dụ: y = 2x – 3 là hàm số bậc nhất với a = 2 và b = -3 y = x + 4 là hàm số bậc nhất với a = 1, b = 4 2. Đồ thị của hàm số y = ax + b (a\( \ne \)0) Hàm số y = ax (a\( \ne \)0, b = 0) Đồ thị của hàm số y = ax (a\( \ne \)0) là một đường thẳng đi qua gốc tọa độ O(0;0). Đồ thị hàm số y = ax (a\( \ne \)0) luôn đi qua gốc tọa độ nên khi vẽ đồ thị này, ta chỉ cần xác định thêm một điểm khác O. Chú ý: Đồ thị của hàm số y = ax còn được gọi là đường thẳng y = ax.
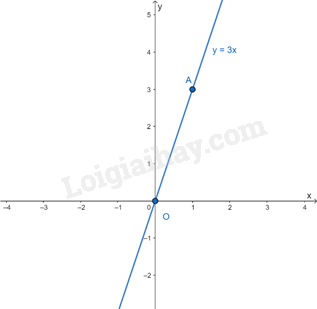
Ví dụ: Cho hàm số y = 3x. Cho x = 1 ta có y = 3. Ta vẽ điểm A(1; 3) Đồ thị hàm số y = 3x là đường thẳng OA Hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0) Đồ thị của hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0) là một đường thẳng song song với đường thẳng y = ax khi b \( \ne \) 0. Để vẽ đồ thị hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0), ta chỉ cần xác định hai điểm phân biệt thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Lưu ý: - Khi vẽ đồ thị của hàm số y = ax + b (a\( \ne \)0), người ta thường vẽ đường thẳng đi qua hai điểm M(0;b) thuộc trục tung Oy và điểm \(N\left( {\frac{{ - b}}{a};0} \right)\) thuộc trục hoành Ox.
- Khi b = 0 thì y = ax và đồ thị của hàm số là đường thẳng đi qua gốc tọa độ O(0; 0). - Đồ thị của hàm số y = ax + b (a\( \ne \)0) còn được gọi là đường thẳng y = ax + b.
|