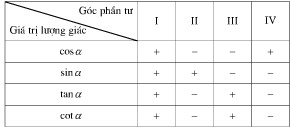
Lý thuyết giá trị lượng giác của một cung

1. Định nghĩa

Trên đường tròn lượng giác cho cung $\overparen{AM}$ có số đo $sđ\overparen{AOM}= α$ thì:

+ Tung độ của $M$ gọi là $\sin$ của $α$, kí hiệu $\sin α$: $\overline {OQ}= \sinα$

+ Hoành độ của $M$ gọi là cosin của $α$, kí hiệu là $\cosα$: $\overline {OP}= \cosα$

+ Nếu $cosα \ne 0$, ta gọi là tang của $α$, kí hiệu $tanα$ là tỉ số: ${{\sin \alpha } \over {cos\alpha }} = \tan \alpha$

+ Nếu $\sinα \ne 0$, ta gọi là cotang của $α$, kí hiệu là: ${{{\rm{cos}}\alpha } \over {\sin \alpha }} = \cot \alpha$

Ghi chú: Vì $sđ\overparen{AM} =sđ\overparen{(OA, OM)}$ nên định nghĩa các giá trị lượng giác của cung lượng giác $α$ cũng là giá trị lượng giác của góc lượng giác $α$.

2. Hệ quả

a) $-1 ≤ sinα ≤ 1, -1 ≤ cosα ≤ 1 ;$$∀α \in\mathbb R$ 

$\sin(α + k2π) = \sinα ;∀k \in \mathbb R$

$cos(α + k2π) = cosα ,∀k \in\mathbb R$

b) $tanα$ xác định với mọi$α \ne {\pi\over 2} + kπ, k \in\mathbb Z$

$cotα$ xác định với mọi $α \ne kπ, k \in\mathbb Z$

                $tan(α + kπ) = tanα ,∀k\in\mathbb R$

               $cot(α + kπ) = cotα ,∀k \in\mathbb R$

c) Bảng xác định dấu của các giá trị lượng giác

d) Các hệ thức lượng giác cơ bản:

$si{n^2}\alpha {\rm{ }} + {\rm{ }}co{s^2}\alpha {\rm{ }} = {\rm{ }}1$;

$tanα.cotα = 1$

$1 + {\tan ^2}\alpha  = {1 \over {{\rm{co}}{{\rm{s}}^2}\alpha }}$

$1 + {\cot ^2}\alpha  = {1 \over {{{\sin }^2}\alpha }}$

3. Giá trị lượng giác của các cung có liên quan đặc biệt

a) Cung đối nhau: $α$ và $(-α)$

$sin(-α) = -sinα$                   $tan(-α) = -tanα$

$cos(-α) = cosα$                       $cot(-α) = -cotα$

b) Cung bù nhau: $α$ và $π - α$

$sin(π - α) = sinα$                         $tan(π - α) = -tanα$

$cos(π - α) = -cosα$                            $cot(π - α) = -cotα$

c) Cung hơn nhau $π$: $α$ và $π + α$ 

$sin(π + α) = -sinα$                   $tan(π + α) = tanα$

$cos(π + α) = -cosα$                 $cot(π + α) = cotα$

d) Cung phụ nhau: $α$ và ${\pi  \over 2} - \alpha$

$sin\left( {{\pi  \over 2} - \alpha } \right) = cosα$                                $tan\left( {{\pi  \over 2} - \alpha } \right)= cosα$

$cos \left( {{\pi  \over 2} - \alpha } \right) = sinα$                              $cos=\left( {{\pi  \over 2} - \alpha } \right) = tan α$

HocTot.Nam.Name.Vn