Lý thuyết Dãy số - SGK Toán 11 Chân trời sáng tạo

1. Định nghĩa dãy số

• Dãy số vô hạn

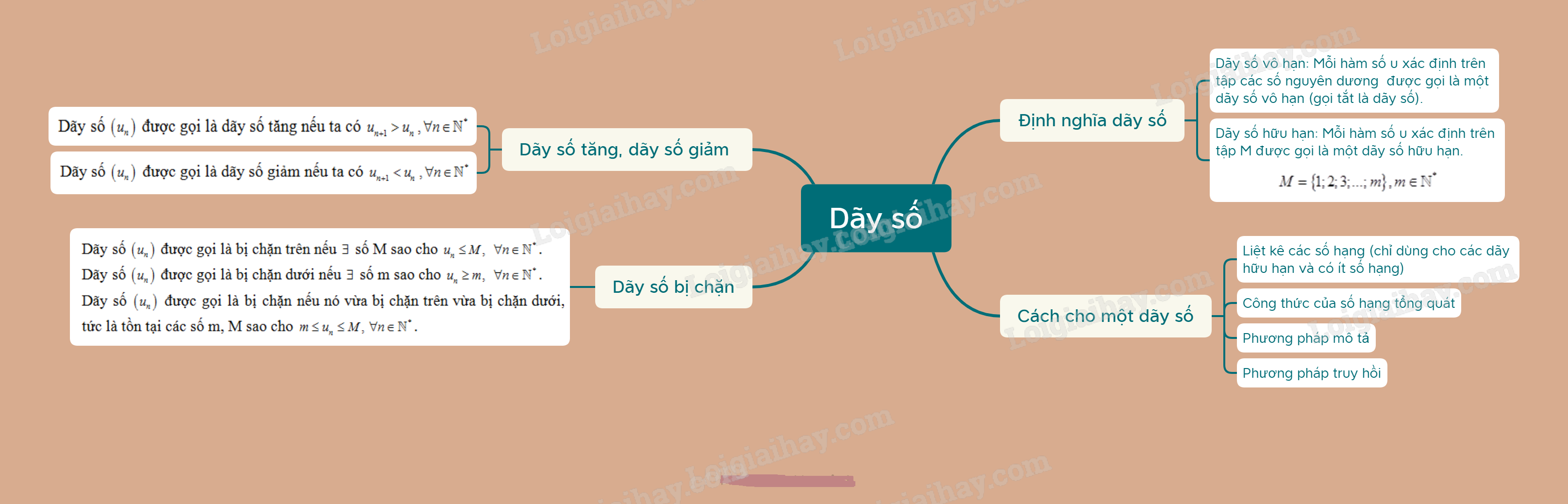
- Hàm số u xác định trên tập các số nguyên dương ${\mathbb{N}^*}$được gọi là một dãy số vô hạn (gọi tắt là dãy số), nghĩa là

$u:{\mathbb{N}^*} \to \mathbb{R}$

$n \mapsto {u_n} = u\left( n \right)$

  Dãy số trên được kí hiệu là $\left( {{u_n}} \right)$.

- Dãy số $\left( {{u_n}} \right)$được viết dưới dạng khai triển ${u_1},{u_2},{u_3},...,{u_n},...$

- Số ${u_1}$ là số hạng đầu; ${u_n}$là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

*Chú ý: Nếu $\forall n \in {\mathbb{N}^*},{u_n} = c$thì $\left( {{u_n}} \right)$được gọi là dãy số không đổi.

• Dãy số hữu hạn

Mỗi hàm số u xác định trên tập $M = \left\{ {1;2;3;...;m} \right\},m \in {\mathbb{N}^*}$ được gọi là một dãy số hữu hạn.Dạng khai triển của dãy số hữu hạn là ${u_1},{u_2},{u_3},...,{u_m}$.

Trong đó, số ${u_1}$ gọi là số hạng đầu, ${u_m}$là số hạng cuối.

2. Cách cho một dãy số

Một dãy số có thể cho bằng:

• Liệt kê các số hạng (với các dãy hữu hạn).
• Công thức của số hạng tổng quát ${u_n}$.
• Phương pháp truy hồi:

- Cho số hạng thứ nhất ${u_1}$ (hoặc một vài số hạng đầu tiên)

- Cho một công thức tính ${u_n}$ theo${u_{n - 1}}$ (hoặc theo vài số hạng đứng ngay trước nó).

• Phương pháp mô tả.

3. Dãy số tăng, dãy số giảm

• Dãy số $\left( {{u_n}} \right)$ được gọi là dãy số tăng nếu ta có ${u_{n + 1}} > {u_n}$$,\forall n \in {\mathbb{N}^*}$.
• Dãy số $\left( {{u_n}} \right)$ được gọi là dãy số giảm nếu ta có ${u_{n + 1}} < {u_n}$$,\forall n \in {\mathbb{N}^*}$.

4. Dãy số bị chặn

• Dãy số $\left( {{u_n}} \right)$ được gọi là bị chặn trên nếu $\exists$ số M sao cho ${u_n} \le M,$ $\forall n \in {\mathbb{N}^*}$.
• Dãy số $\left( {{u_n}} \right)$ được gọi là bị chặn dưới nếu $\exists$ số m sao cho ${u_n} \ge m,$ $\forall n \in {\mathbb{N}^*}$.
• Dãy số $\left( {{u_n}} \right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho $m \le {u_n} \le M,$$\forall n \in {\mathbb{N}^*}$.