Lý thuyết Các số đặc trưng đo độ phân tán - SGK Toán 10 Kết nối tri thức1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ 2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN 3. PHÁT HIỆN SỐ LIỆU BẤT THƯỜNG HOẶC KHÔNG CHÍNH XÁC BẰNG BIỂU ĐỒ HỘP Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... 1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ a. Khoảng biến thiên Khoảng biến thiên (hay biên độ) = Giá trị lớn nhất – Giá trị nhỏ nhất. Ý nghĩa: Dùng để đo độ phân tán của mẫu số liệu: Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán (càng không đồng đều) Nhận xét: Đơn giản, dễ tính toán nhưng bỏ qua thông tin từ các giá trị khác và bị ảnh hưởng bởi các giá trị bất thường. b. Khoảng tứ phân vị Khoảng tứ phân vị (hay độ trải giữa): \({\Delta _Q} = {Q_3} - {Q_1}\) Ý nghĩa: Dùng để đo độ phân tán của mẫu số liệu: Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán (càng không đồng đều) Nhận xét: Chỉ sử dụng thông tin của 50% số liệu chính giữa nhưng không bị ảnh hưởng bởi các giá trị bất thường.
2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN Có một vài số đặc trưng khác đo độ phân tán sử dụng thông tin của tất cả các giá trị trong mẫu. Hai trong số đó là phương sai và độ lệch chuẩn. Cho mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\), số trung bình là \(\overline x \) Độ lệch của mỗi giá trị: \({x_i} - \overline x \) Phương sai: \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) Độ lệch chuẩn: \(s = \sqrt {{s^2}} \) Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn Chú ý: Phương sai của mẫu số liệu cho dạng bảng tần số: \({s^2} = \frac{{{m_1}{{({x_1} - \overline x )}^2} + {m_2}{{({x_2} - \overline x )}^2} + ... + {m_k}{{({x_k} - \overline x )}^2}}}{n}\) Với \({m_i}\) là tần số của giá trị \({x_i}\) và \(n = {m_1} + {m_2} + ... + {m_k}\)
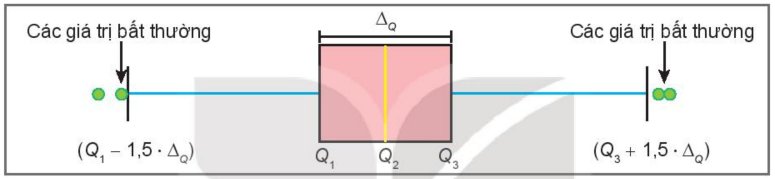
3. PHÁT HIỆN SỐ LIỆU BẤT THƯỜNG HOẶC KHÔNG CHÍNH XÁC BẰNG BIỂU ĐỒ HỘP +) Giá trị bất thường: là những giá trị quá lớn hoặc quá nhỏ so với đa số các giá trị khác. +) Biểu đồ hộp \( \Rightarrow x\) là giá trị bất thường nếu \(\left[ \begin{array}{l}x < {Q_1} - 1,5.{\Delta _Q}\\x > {Q_3} + 1,5.{\Delta _Q}\end{array} \right.\)
|