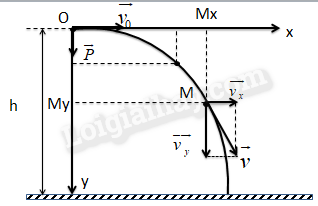
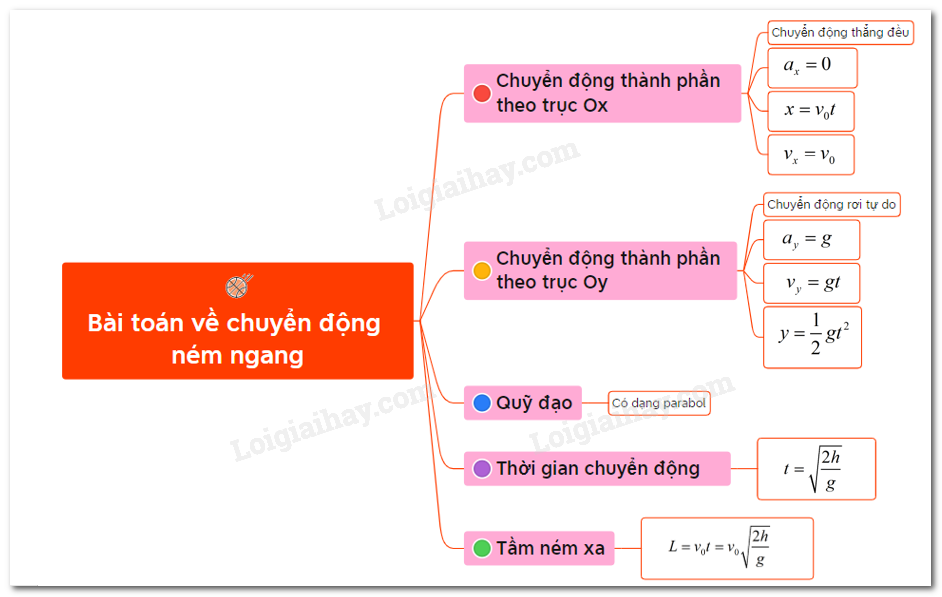
Lý thuyết bài toán về chuyển động ném ngangA. TÓM TẮT LÍ THUYẾT GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn I. Khảo sát chuyển động ném ngang 1. Chọn hệ trục tọa độ và gốc thời gian - Chọn hệ trục tọa độ xOy, trục Ox hướng theo vecto vận tốc →v0, trục Oy hướng theo vecto trọng lực →P. - Gốc thời gian là lúc bắt đầu ném. 2. Phân tích chuyển động ném ngang - Chuyển động ném ngang có thể phân tích thành hai chuyển động thành phần theo hai trục tọa độ. Chuyển động của các hình chiếu Mx và My trên các trục Ox và Oy gọi là các chuyển động thành phần của vật M. + Chuyển động thành phần theo trục Ox là chuyển động thẳng đều với các phương trình: {v0x=v0ax=0vx=0 + Chuyển động thành phần theo trục Oy là chuyển động rơi tự do với các phương trình: {v0y=0ay=gvy=gt + Phương trình chuyển động của vật là: {x=v0ty=gt22 II. Xác định chuyển động của vật - Khử t giữa hai phương trình x = v0t và y = 12gt2, ta được: Phương trình quỹ đạo của vật là: y=g2v20x2 Như vậy, quỹ đạo của chuyển động ném ngang là đường Parabol. - Phương trình vận tốc: v=√(gt)2+v20 - Thời gian chuyển động của vật ném ngang bằng thời gian rơi tự do từ cùng một độ cao h và được xác định: y = 12gt2 = h => t = √2hg + Tầm xa L = xmax = v0.t = v0√2hg Sơ đồ tư duy về bài toán chuyển động ném ngang
|