Lý thuyết: Bài toán và thuật toán trang 32 SGK Tin học 10

1. Khái niệm bài toán

- Bài toán là một việc nào đó mà con người muốn máy tính thực hiện.

- Các yếu tố của một bài toán:

   + Input: Thông tin đã biết, thông tin đưa vào máy tính.

   + Output: Thông tin cần tìm, thông tin lấy ra từ máy tính.

- Ví dụ: Bài toán tìm ước chung lớn nhất của 2 số nguyên dương, khi đó:

   + Input: hai số nguyên dương A, B.

   + Output: ước chung lớn nhất của A và B

2. Khái niệm thuật toán

a) Khái niệm

Thuật toán là 1 dãy hữu hạn các thao tác được sắp xếp theo 1 trình tự xác định sao cho sau khi thực hiện dãy thao tác ấy, từ Input của bài toán, ta nhận được Output cần tìm.

b) Biểu diễn thuật toán

- Sử dụng cách liệt kê: nêu ra tuần tự các thao tác cần tiến hành.

- Sử dụng sơ đồ khối để mô tả thuật toán. 

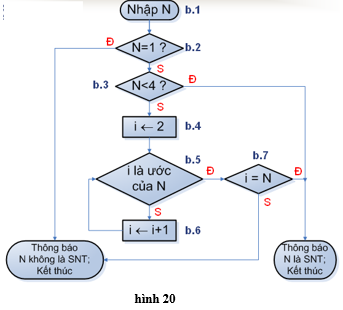
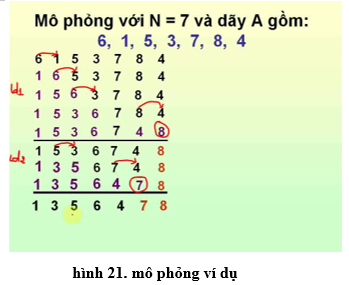
c) Các tính chất của thuật toán

- Tính dừng: thuật toán phải kết thúc sau 1 số hữu hạn lần thực hiện các thao tác.

- Tính xác định: sau khi thực hiện 1 thao tác thì hoặc là thuật toán kết thúc hoặc là có đúng 1 thao tác xác định để được thực hiện tiếp theo.

- Tính đúng đắn: sau khi thuật toán kết thúc, ta phải nhận được Output cần tìm.

3. Một số ví dụ về thuật toán

Ví dụ 1: Kiểm tra tính nguyên tố của 1 số nguyên dương

• Xác định bài toán

- Input: N là một số nguyên dương;

- Output: ″N là số nguyên tố″ hoặc ″N không là số nguyên tố″.

• Ý tưởng:

- Định nghĩa: ″Một số nguyên dương N là số nguyên tố nếu nó chỉ có đúng hai ước là 1 và N″

- Nếu N = 1 thì N không là số nguyên tố.

- Nếu 1 < N < 4 thì N là số nguyên tố.

- N ≥ 4: Tìm ước i đầu tiên > 1 của N.

+ Nếu i < N thì N không là số nguyên tố (vì N có ít nhất 3 ước 1, i, N).

+ Nếu i = N thì N là số nguyên tố.

• Xây dựng thuật toán

a) Cách liệt kê

   - Bước 1: Nhập số nguyên dương N;

   - Bước 2: Nếu N=1 thì thông báo ″N không là số nguyên tố″, kết thúc;

   - Bước 3: Nếu N<4 thì thông báo ″N là số nguyên tố″, kết thúc;

   - Bước 4: i ← 2;

   - Bước 5: Nếu i là ước của N thì đến bước 7;

   - Bước 6: i ← i+1 rồi quay lại bước 5; (Tăng i lên 1 đơn vị)

   - Bước 7: Nếu i = N thì thông báo ″N là số nguyên tố″, ngược lại thì thông báo ″N không là số nguyên tố″, kết thúc;

b) Sơ đồ khối

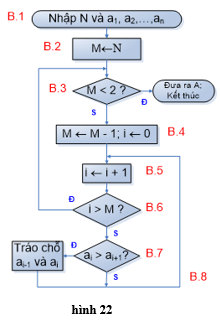
Lưu ý: Nếu N >= 4 và không có ước trong phạm vi từ 2 đến phần nguyên căn bậc 2 của N thì N là số nguyên tố.

Ví dụ 2: Sắp xếp bằng cách tráo đổi

• Xác định bài toán

   - Input: Dãy A gồm N số nguyên a1, a2,…, an

   - Output: Dãy A được sắp xếp thành dãy không giảm.

• Ý tưởng

   - Với mỗi cặp số hạng đứng liền kề trong dãy, nếu số trước lớn hơn số sau ta đổi chỗ chúng cho nhau. (Các số lớn sẽ được đẩy dần về vị trí xác định cuối dãy).

   - Việc này lặp lại nhiều lượt, mỗi lượt tiến hành nhiều lần so sánh cho đến khi không có sự đổi chỗ nào xảy ra nữa.

• Xây dựng thuật toán

a) Cách liệt kê

   - Bước 1: Nhập N, các số hạng a1, a2,…, an;

   - Bước 2: M ← N;

   - Bước 3: Nếu M < 2 thì đưa ra dãy A đã được sắp xếp, rồi kết thúc;

   - Bước 4: M ← M – 1, i ← 0;

   - Bước 5: i ← i + 1;

   - Bước 6: Nếu i > M thì quay lại bước 3;

   - Bước 7: Nếu ai > ai+1 thì tráo đổi ai và ai+1 cho nhau;

   - Bước 8: Quay lại bước 5;

b) Sơ đồ khối

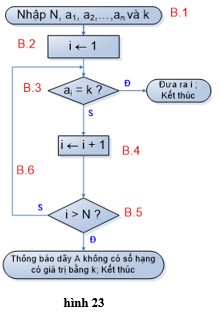
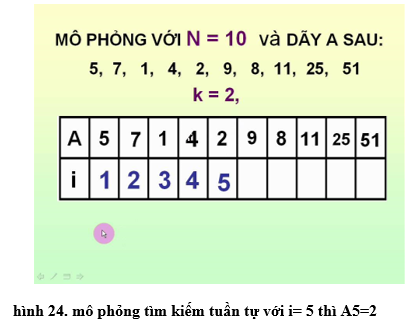
Ví dụ 3: Bài toán tìm kiếm

• Xác định bài toán

- Input : Dãy A gồm N số nguyên khác nhau a1, a2,…, an và một số nguyên k (khóa)

   Ví dụ : A gồm các số nguyên ″ 5 7 1 4 2 9 8 11 25 51″ và k = 2 (k = 6).

- Output: Vị trí i mà ai = k hoặc thông báo không tìm thấy k trong dãy. Vị trí của 2 trong dãy là 5 (không tìm thấy 6)

• Ý tưởng

Tìm kiếm tuần tự được thực hiện một cách tự nhiên: Lần lượt đi từ số hạng thứ nhất, ta so sánh giá trị số hạng đang xét với khóa cho đến khi gặp một số hạng bằng khóa hoặc dãy đã được xét hết mà không tìm thấy giá trị của khóa trên dãy.

• Xây dựng thuật toán

a) Cách liệt kê

   - Bước 1: Nhập N, các số hạng a1, a2,…, aN và giá trị khoá k;

   - Bước 2: i ← 1;

   - Bước 3: Nếu ai = k thì thông báo chỉ số i, rồi kết thúc;

   - Bước 4: i ←i+1;

   - Bước 5: Nếu i > N thì thông báo dãy A không có số hạng nào có giá trị bằng k, rồi kết thúc;

   - Bước 6: Quay lại bước 3;

b) Sơ đồ khối

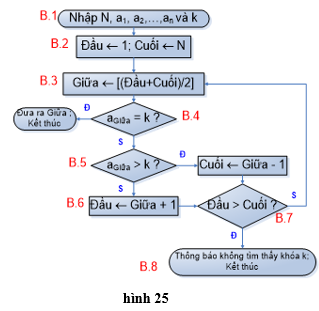
Ví dụ 4: Tìm kiếm nhị phân

• Xác định bài toán

- Input: Dãy A là dãy tăng gồm N số nguyên khác nhau a1, a2,…, an và một số nguyên k.

Ví dụ: Dãy A gồm các số nguyên 2 4 5 6 9 21 22 30 31 33 và k = 21 (k = 25)

- Output : Vị trí i mà ai = k hoặc thông báo không tìm thấy k trong dãy. Vị trí của 21 trong dãy là 6 (không tìm thấy 25)

• Ý tưởng

Sử dụng tính chất dãy A đã sắp xếp tăng, ta tìm cách thu hẹp nhanh vùng tìm kiếm bằng cách so sánh k với số hạng ở giữa phạm vi tìm kiếm (agiữa), khi đó chỉ xảy ra một trong ba trường hợp:

   - Nếu agiữa= k thì tìm được chỉ số, kết thúc;

   - Nếu agiữa > k thì việc tìm kiếm thu hẹp chỉ xét từ adầu (phạm vi) → agiữa - 1;

   - Nếu agiữa < k việc tìm kiếm thu hẹp chỉ xét từ agiữa + 1→acuối (phạm vi).

Quá trình trên được lặp lại cho đến khi tìm thấy khóa k trên dãy A hoặc phạm vi tìm kiếm bằng rỗng.

• Xây dựng thuật toán

a) Cách liệt kê

   - Bước 1: Nhập N, các số hạng a1, a2,…, aN và giá trị khoá k;

   - Bước 2: Đầu ←1; Cuối ←N;

   - Bước 3: Giữa←[(Đầu+Cuối)/2];

   - Bước 4: Nếu agiữa = k thì thông báo chỉ số Giữa, rồi kết thúc;

   - Bước 5: Nếu agiữa > k thì đặt Cuối = Giữa - 1 rồi chuyển sang bước 7;

   - Bước 6: Đầu ←Giữa + 1;

   - Bước 7: Nếu Đầu > Cuối thì thông báo không tìm thấy khóa k trên dãy, rồi kết thúc;

   - Bước 8: Quay lại bước 3.

b) Sơ đồ khối

HocTot.Nam.Name.Vn