Lí thuyết Bài 1 Chuyển động tròn - Vật lí 10Mô tả chuyển động tròn Lực hướng tâm và gia tốc hướng tâm Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... BÀI 1: CHUYỂN ĐỘNG TRÒN I. Mô tả chuyển động tròn - Một vật thực hiện chuyển động tròn khi nó di chuyển trên một đường tròn - Ví dụ: Đầu kim đồng hồ chuyển động trên mặt số
1. Độ dịch chuyển góc và tốc độ góc
- Giả sử một vật chuyển động trên một đường tròn bán kính r. Trong thời gian t vật đi được quãng đường s. Góc θ ứng với cung tròn s mà vật đã đi được kể từ vị trí ban đầu gọi là độ dịch chuyển góc. Độ dịch chuyển góc θ được xác định: + Đơn vị: rad (radian) + Nếu s=r thì θ=1 rad - Đại lượng được xác dịnh bởi độ dịch chuyển góc trong một đơn vị thời gian gọi là tốc độ góc.
+ Đơn vị: rad/s 2. Tốc độ và vận tốc của chuyển động tròn đều - Một vật chuyển động tròn đều khi nó di chuyển trên một đường tròn với vận tốc không đổi, tức là vật dịch chuyển được các cung tròn có số đo góc như nhau sau những khoảng thời gian bằng nhau - Tốc độ của chuyển động tròn đều là không đổi \(v = \frac{{2\pi r}}{T}\) Trong đó: r là bán kính của đường tròn (m) T là thời gian vật đi hết một vòng (s) - Vận tốc của chuyển động tròn tại một điểm trên quỹ đạo có phương tiếp tuyến với quỹ đạo tại điểm đó 3. Liên hệ giữa tốc độ và tốc độ góc Tốc độ = tốc độ góc x bán kính hay v=ωr II. Lực hướng tâm và gia tốc hướng tâm 1. Lực hướng tâm - Lực hướng tâm là lực tác dụng lên vật luôn hướng vào tâm quỹ đạo tròn 2. Gia tốc hướng tâm - Theo Định luật II Newton lực hướng tâm gây ra gia tốc cho vật, gia tốc này có cùng hướng với hướng của lực hướng tâm, nghĩa là luôn hướng vào tâm của quỹ đạo nên được gọi là gia tốc hướng tâm \(a = \frac{{{v^2}}}{r} = r{\omega ^2}\) 3. Lực hướng tâm và một số tính huống chuyển động tròn trong thực tế
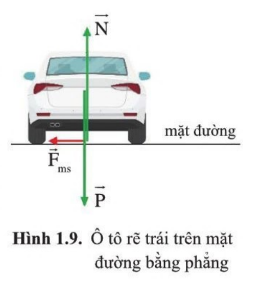
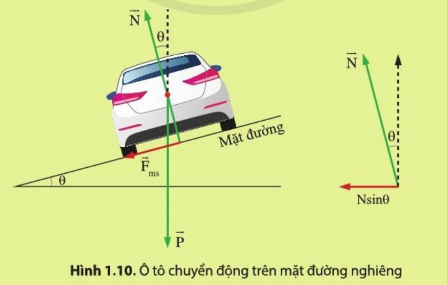
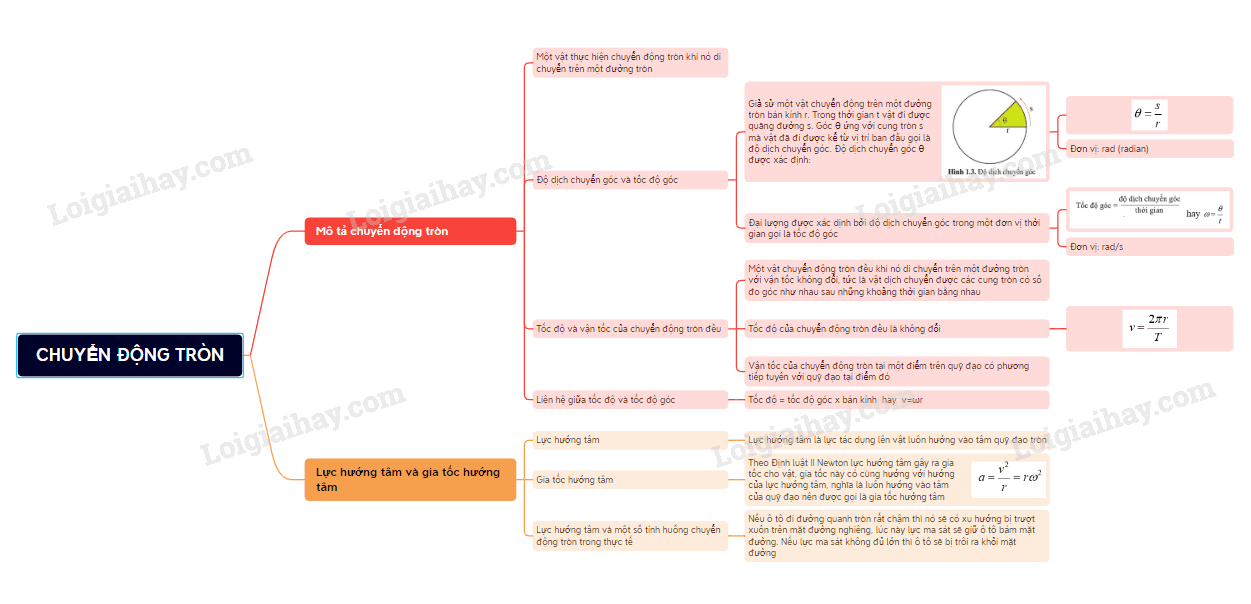
- Nếu ô tô đi đường quanh tròn rất chậm thì nó sẽ có xu hướng bị trượt xuốn trên mặt đường nghiêng, lúc này lực ma sát sẽ giữ ô tô bám mặt đường. Nếu lực ma sát không đủ lớn thì ô tô sẽ bị trôi ra khỏi mặt đường Sơ đồ tư duy về “Chuyển động tròn”
|














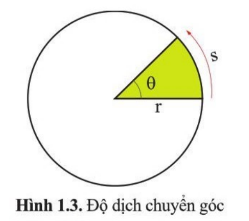
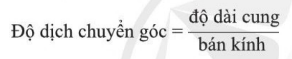 hay \(\theta = \frac{s}{r}\)
hay \(\theta = \frac{s}{r}\)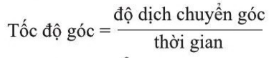 hay \(\omega = \frac{\theta }{t}\)
hay \(\omega = \frac{\theta }{t}\)