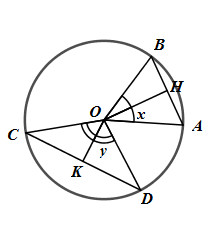
Hoạt động 7 trang 77 Tài liệu dạy – học Toán 9 tập 2Giải bài tập Cho đường tròn (O; R) với hai góc ở tâm Đề bài Cho đường tròn (O; R) với hai góc ở tâm ^AOB=2x và ^COD=2y sao cho y > x. Gọi H và K lần lượt là trung điểm của AB và CD. Hãy chứng minh AH = R.sinx và CK = R.siny. So sánh AB và CD. Lời giải chi tiết +) Xét tam giác OAB có OA=OB=R⇒ΔOAB cân tại O ⇒ Đường trung tuyến OH đồng thời là đường cao và đường phân giác của góc ^AOB ⇒OH⊥AB và ^AOH=^BOH=2x2=x Xét tam giác vuông OAH có: AH=OA.sin^AOH=Rsinx. Chứng minh hoàn toàn tương tự ta có CK=Rsiny. +) Vì H là trung điểm của AB ⇒AB=2AH=2Rsinx Vì K là trung điểm của CD ⇒CD=2CK=2Rsiny Do y>x⇒siny>sinx ⇒2Rsiny>2Rsinx⇒CD>AB. Vậy CD>AB. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
|
