Bài 4. Sóng dừng trang 54, 55, 56, 57, 58, 59, 60 Vật Lí 11 Cánh diềuMột sợi dây đàn hồi có một đầu cố định. Làm cho đầu tự do của dây dao động thì có những lúc ta thấy trên dây xuất hiện những điểm đứng yên. Những điểm đứng yên này có giống với những điểm đứng yên trong hiện tượng giao thoa của sóng nước? Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
Câu hỏi tr 54 KĐ Một sợi dây đàn hồi có một đầu cố định. Làm cho đầu tự do của dây dao động thì có những lúc ta thấy trên dây xuất hiện những điểm đứng yên. Những điểm đứng yên này có giống với những điểm đứng yên trong hiện tượng giao thoa của sóng nước? Vì sao dao động tại những điểm đó lại triệt tiêu nếu chỉ nhận sóng từ đầu dao động truyền đến?
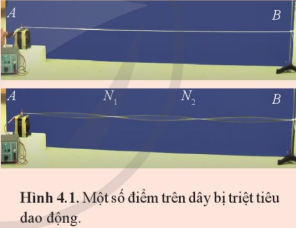
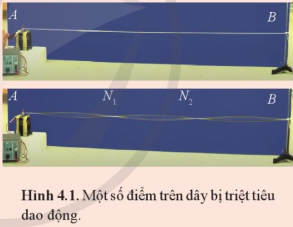
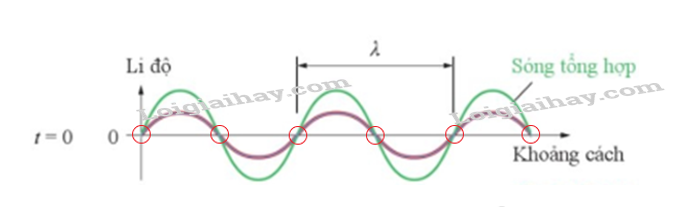
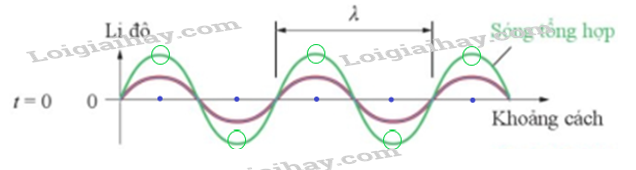
Phương pháp giải: Dựa vào kiến thức về giao thoa sóng để giải thích. Lời giải chi tiết: Những điểm đứng yên giống như những điểm đứng yên trong hiện tượng giao thoa của sóng nước. Dao động tại những điểm đó triệt tiêu là do sự giao thoa của hai sóng, ngoài sóng tới còn có sóng phản xạ. Câu hỏi tr 55 CH 1 Hãy chỉ ra các nút sóng và các bụng sóng trên các Hình 4.1 và 4.2.
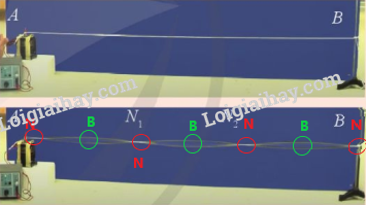
Phương pháp giải: Dựa vào định nghĩa về bụng sóng và nút sóng: Khi có sóng dừng, những điểm đứng yên là nút sóng, những điểm ở chính giữa hai nút sóng liên tiếp là những điểm dao động với biên độ lớn nhất gọi là bụng sóng. Lời giải chi tiết: Những điểm đứng yên là nút sóng, những điểm ở chính giữa hai nút sóng liên tiếp là những điểm dao động với biên độ lớn nhất gọi là bụng sóng. Kí hiệu trên hình: màu đỏ - N: nút sóng; màu xanh – B: bụng sóng Câu hỏi tr 55 CH 2 Tiến hành thí nghiệm tạo sóng dừng trên dây và lập bảng ghi kết quả vào vở như Bảng 4.1.
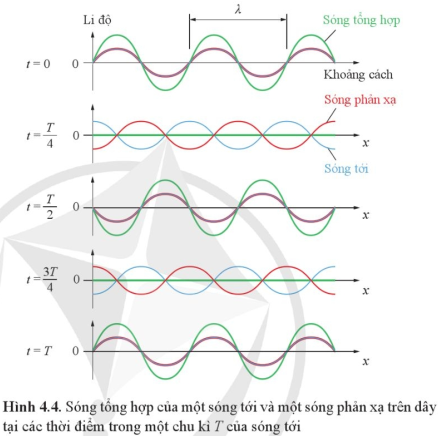
Nhận xét về mối liên hệ giữa tần số sóng trên dây và số bụng sóng quan sát được. Phương pháp giải: Từ kết quả có được về tần số và số bụng sóng quan sát được, nêu ra mối liên hệ. Lời giải chi tiết: Tần số sóng trên dây càng lớn, số bụng sóng càng nhiều. Số bụng sóng tỉ lệ với tần số sóng. Câu hỏi tr 56 CH 1 Hãy chỉ ra vị trí các nút sóng trên Hình 4.4. Xác định khoảng cách giữa hai nút sóng liên tiếp.
Phương pháp giải: Xác định vị trí của các nút sóng, chọn hai nút sóng liên tiếp và biểu diễn khoảng cách giữa chúng theo λ. Lời giải chi tiết: Nút sóng là những điểm đứng yên. Trong hình vẽ, các nút sóng là giao điểm của đồ thị sóng tổng hợp với trục Ot (li độ của các điểm nút luôn bằng 0). Từ hình vẽ ta thấy, khoảng cách giữa hai nút sóng là λ2, nửa bước sóng. Câu hỏi tr 56 CH 2 Hãy chỉ ra vị trí các bụng sóng trên Hình 4.4. So sánh biên độ của sóng tổng hợp tại bụng sóng với biên độ của sóng tới.
Phương pháp giải: Chỉ ra vị trí của các bụng sóng và so sánh biên độ dao động tại những điểm này với biên độ dao động của sóng tới. Lời giải chi tiết: Vị trí của các bụng sóng là tại các điểm chính giữa hai nút sóng. Biên độ dao động tại các bụng sóng gấp đôi biên độ dao động của sóng tới. Câu hỏi tr 56 CH 3 Có thể nói sóng dừng trên dây là hiện tượng giao thoa sóng được không? Nếu có thì đây là giao thoa của những sóng nào? Phương pháp giải: Dựa vào kiến thức về giao thoa sóng và giải thích về sự tạo thành sóng dừng. Lời giải chi tiết: Có thể nói sóng dừng trên dây là hiện tượng giao thoa sóng. Đây là giao thoa của sóng tới và sóng phản xạ. Câu hỏi tr 57 CH 1 Kiểm tra lại công thức (4.4) với kết quả của Bảng 4.1 thu được trong thí nghiệm quan sát sóng dừng trên dây đã thực hiện. Phương pháp giải: Công thức (4.4): L=kλ2. Xác định bước sóng λqua công thức liên hệ với tần số. Lời giải chi tiết: Xác định bước sóng λ: λ=vf. Tính thương số Lλ2=2Lλ, nếu kết quả là một số nguyên thì công thức (4.4) đúng với thí nghiệm này. Câu hỏi tr 57 CH 2 Từ công thức tính tốc độ sóng, hãy chỉ ra các đại lượng cần xác định khi muốn đo tốc độ truyền âm trong không khí. Phương pháp giải: Dựa vào công thức tính tốc độ sóng: v=fλđể chỉ ra đại lượng cần xác định. Lời giải chi tiết: Công thức tính tốc độ sóng: v=fλ. Do đó, để xác định tốc độ truyền âm trong không khí, cần xác định tần số sóng và bước sóng. Câu hỏi tr 57 CH 3 Đề xuất phương án ứng dụng hiện tượng sóng dừng để đo tốc độ truyền âm trong không khí: - Vì sao một đầu của ống cộng hướng cần dịch chuyển được? Tìm phương án giúp thay đổi độ dài của cột khí trong ống. - Vì sao cần xác định các vị trí mà âm thanh thu được có cường độ nhỏ nhất hoặc lớn nhất? - Nêu cách tính bước sóng của sóng âm qua các giá trị độ dài cột khí trong ống của những lần xác định được vị trí nút sóng. Phương pháp giải: Dựa vào các đặc điểm của sóng dừng. Để xác định tốc độ truyền âm trong không khí cần xác định tần số sóng và bước sóng. Lời giải chi tiết: - Một đầu của ống cộng hưởng cần dịch chuyển được để thay đổi chiều dài của ống cộng hưởng. Để thay đổi độ dài của cột khí trong ống, có thể đặt một pít-tông vừa khít vào trong ống nhựa, ta đẩy hoặc kéo pít-tông để thay đổi độ dài cột khí. - Cần xác định các vị trí mà âm thanh thu được có cường độ nhỏ nhất hoặc lớn nhất để xác định độ dài của cột khí là L=kλ2hoặc L=(2k+1)λ4. - Ở của những lần xác định được vị trí nút sóng với cùng một tần số, độ dài cột khí trong ống L=kλ2 . Lấy hai giá trị độ dài L1,L2sao cho L1−L2nhỏ nhất. Khi đó, L1=kλ2 và L2=(k−1)λ2nên L1−L2=λ2⇒λ=2(L1−L2). Câu hỏi tr 58 CH 1 Tiến hành thí nghiệm và lập bảng ghi kết quả như mẫu Bảng 4.2. Tính sai số của phép đo Phương pháp giải: Dùng công thức tính sai số tuyệt đối và sai số tương đối của phép đo gián tiếp. Lời giải chi tiết: Tính sai số Δd. Khi đó, do bước sóng được tính theo công thức λ=2dnên Δλ=2Δd. Tốc độ truyền sóng v=λf. Suy ra δv=δλ+δf. Tính Δv=ˉv.δv. Câu hỏi tr 58 CH 2 Vì sao ở thí nghiệm tạo sóng dừng trong ống cộng hưởng nếu một đầu ống để hở thì khi có sóng dừng ta có thể nghe được âm rất to tại đầu ống đó? Phương pháp giải: Dựa vào đặc điểm của sóng dừng khi một đầu ống tự do, không cố định. Lời giải chi tiết: Nếu một đầu ống để hở, khi có sóng dừng, đầu ống này không đóng vai trò là nút sóng nữa mà là một bụng sóng. Tại bụng sóng, biên độ sóng là lớn nhất, nên cường độ sóng âm lớn nhất (vì cường độ sóng tỉ lệ với bình phương biên độ sóng). Do đó, ta có thể nghe được âm rất to tại đầu ống này. Bài tập CĐ 2 Bài 1 Cho sơ đồ một số phân tử không khí khi có một sóng âm truyền qua như Hình 1.1 a) Vẽ lại sơ đồ trên vào vở và đánh dấu một vùng sóng cho thấy khí bị nén (đánh dấu bằng điểm N) b) Đánh dấu một vùng sóng cho thấy khí giãn (đánh dấu bằng điểm G). c) Sóng âm có tần số 240 Hz. Điều này có ý nghĩa gì đối với mỗi phân tử không khí? d) Tốc độ sóng âm là 320 m/s. Tính bước sóng của sóng âm.
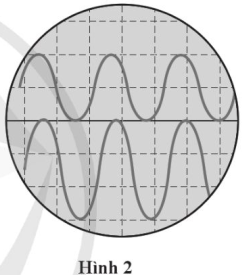
Phương pháp giải: Quan sát sơ đồ, đánh dấu vùng sóng cho thấy khí bị nén (khoảng cách giữa các phần tử gần nhau hơn) và vùng sóng cho thấy khí bị giãn (khoảng cách giữa các phần tử xa nhau hơn). Nêu ý nghĩa của tần số sóng đối với dao động của mỗi phân tử. Tính bước sóng của sóng âm bằng công thức λ=vf. Lời giải chi tiết: a) Đánh dấu vùng sóng cho thấy khí bị nén. b) Đánh dấu vùng sóng cho thấy khí giãn. c) Tần số của sóng âm là 240 Hz, sóng âm này làm cho mỗi phần tử không khí có sóng đi qua dao động với tần số 240 Hz. d) Bước sóng của sóng âm là: λ=vf=320240=43(m). Bài tập CĐ 2 Bài 2 Hình 2 cho thấy hai sóng được hiển thị trên một màn hình máy hiện sóng. a) Các sóng có cùng pha hay không? Giải thích. b) Núm điều chỉnh thời gian của màn hình được đặt ở chế độ 500μs/độ chia. Xác định chu kì của mỗi sóng. c) So sánh bước sóng của chúng. d) Tính tỉ lệ cường độ của hai sóng với cùng hệ số khuếch đại.
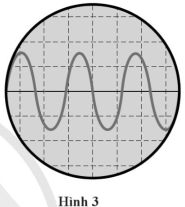
Phương pháp giải: Quan sát, đối chiếu hai đồ thị để xác định hai sóng có cùng pha hay không. Tính chu kì của sóng dựa trên độ chia. Cường độ của sóng tỉ lệ với bình phương của biên độ sóng. Lời giải chi tiết: a) Hai sóng đã cho không cùng pha. Vì đồ thị không ở cùng trạng thái ở cùng một thời điểm. b) Từ đồ thị ta thấy, hai sóng có cùng chu kì. Mỗi chu kì tương ứng với 2,25 độ chia, nên chu kì của hai sóng là: T=2,25.(500.10−6)=1,125.10−3(s). c) Do hai sóng có cùng chu kì T nên tần số của hai sóng là bằng nhau. Tốc độ truyền sóng v của hai sóng là như nhau vì tốc độ truyền sóng chỉ phụ thuộc vào môi trường truyền. Do đó bước sóng của hai sóng λ=vf bằng nhau. d) Với hai sóng có cùng tần số, cường độ của sóng tỉ lệ với bình phương của biên độ sóng. Mà ta thấy A1A2=23 (A1 là biên độ của sóng có đồ thị ở phía trên, A2 là biên độ của sóng có đồ thị ở phía dưới). Do đó, tỉ lệ cường độ của hai sóng với cùng hệ số khuếch đại là: I1I2=(A1A2)2=(23)2=49. Bài tập CĐ 2 Bài 3 Tín hiệu từ một sao nằm trong vùng tử ngoại của quang phổ với bước sóng 7,5.10−8m. Tính tần số của bức xạ này. Phương pháp giải: Tốc độ của ánh sáng là 300 000 km/s. Tìm tần số của bức xạ suy ra từ công thức v=fλ. Lời giải chi tiết: Bức xạ đã cho truyền đi với tốc độ v=300000km/s = 3.108m/s. Tần số của bức xạ là f. Tốc độ sóng là v=fλvới λ=7,5.10−8m. Suy ra, tần số của bức xạ đã cho là: f=vλ=3.1087,5.10−8=4.1015(Hz). Bài tập CĐ 2 Bài 4 Khi xem xét quang phổ thu được từ một thiên thể, các nhà thiên văn nhận thấy các vạch phổ trong vùng ánh sáng nhìn thấy bị dịch về phía ánh sáng đỏ, tức là bước sóng của bức xạ ứng với vạch phổ thu được lớn hơn bước sóng của bức xạ do thiên thể đó phát ra. Hiện tượng này được gọi là sự dịch chuyển đỏ. Vật lí thiên văn ứng dụng sự dịch chuyển đỏ rộng rãi trong việc xác định chuyển động của các thiên thể. Hãy so sánh tần số của bức xạ thu được với tần số của bức xạ do thiên thể phát ra, sau đó cho biết, thiên thể này đang chuyển động như thế nào so với thiết bị thu? Phương pháp giải: Dựa vào so sánh bước sóng của bức xạ thu được với bước sóng của bức xạ do thiên thể phát ra. Khi nguồn sóng và người quan sát chuyển động ra xa nhau thì tần số sóng người quan sát thu được nhỏ hơn tần số do nguồn phát ra. Lời giải chi tiết: Tốc độ sóng là v=fλ. Bức xạ thu được và bức xạ do thiên thể phát ra có sung tốc độ truyền sóng là tốc độ ánh sáng. Do đó, bước sóng tỉ lệ nghịch với tần số. Bước sóng của bức xạ ứng với vạch phổ thu được lớn hơn bước sóng của bức xạ do thiên thể phát ra nên tần số của bức xạ thu được nhỏ hơn tần số của bức xạ do thiên thể phát ra. Tần số của bức xạ thu được nhỏ hơn của bức xạ do thiên thể phát ra, nghĩa là thiên thể này đang chuyển động ra xa khỏi thiết bị thu. Bài tập CĐ 2 Bài 5 Sử dụng công thức tính khoảng vân i=λDatrong thí nghiệm giao thoa ánh sáng Young để giải thích các kết quả quan sát sau: a) Hai khe hẹp càng gần nhau thì các vân trên màn càng xa nhau. b) Các vân giao thoa của ánh sáng lam nằm gần nhau hơn các vân giao thoa ánh sáng đỏ. Phương pháp giải: Dựa vào công thức tính khoảng vân i=λDa, từ sự thay đổi của các đại lượng suy ra sự thay đổi của i. Lời giải chi tiết: a) Hai khe hẹp càng gần nhau thì a càng nhỏ, nên λDa càng lớn, nghĩa là khoảng vâni càng lớn. Mà khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp bằng khoảng vân i nên các vân trên màn càng xa nhau. b) Ánh sáng lam có bước sóng λl<λd, λdlà bước sóng của ánh sáng đỏ. Khi đó, khoảng vân của ánh sáng lam và ánh sáng đỏ lần lượt là il,id: a) il=λlDa<λdDa=id. Khoảng cách giữa hai vân sáng/tối của ánh sáng lam liên tiếp bằng khoảng vân il, giữa hai vân sáng/tối của ánh sáng đỏ liên tiếp bằng id. Do đó, các vân giao thoa của ánh sáng lam nằm gần nhau hơn các vân giao thoa ánh sáng đỏ. Bài tập CĐ 2 Bài 6 Người ta đặt lần lượt các tấm kính lọc trước nguồn phát ánh sáng trắng trong thí nghiệm giao thoa Young. Lúc đầu, khi dùng kính lọc màu đỏ (λđ=640nm) thì khảng vân đo được là 2,4 mm. Khi dùng kính lọc màu làm thì khoảng vân đo được là 1,8 mm. Xác định bước sóng của ánh sáng đi qua kính lọc màu lam. Phương pháp giải: Sử dụng công thức tính khoảng vân i=λDa. Tính tỉ lệ của hai khoảng vân của hai ánh sáng màu. Lời giải chi tiết: Khoảng vân của ánh sáng có bước sóngλlà: i=λDa. Với ánh sáng đỏ có λđ=640nm, khoảng vân là: iđ=λđDa(1); iđ=2,4mm. Với ánh sáng xanh có bước sóng λx, khoảng vân là: ix=λxDa(2); ix=1,8mm. Từ (1)(2) suy ra: idix=λdλx⇒λx=λd.ixid=640.1,82,4=480(nm). Bài tập CĐ 2 Bài 7 Dao động của một nguồn âm được ghi lại trên màn hình máy hiện sóng như Hình 3. a) Xác định tần số của nguồn âm biết đơn vị thời gian trên màn hình được đặt là 1,00 ms/độ chia. b) Đặt nguồn âm này trước miệng một ống cộng hưởng. Thay đổi từ từ chiều dài ống công hưởng. Thay đổi từ từ chiều dài ống cộng hưởng, đồng thời cho nguồn phát âm thanh thì thấy, giữa hai lần liên tiếp nghe được âm rất to tại miệng ống, chiều dài ống cộng hưởng đã thay đổi một khoảng là 0,32 m. Hãy xác định tốc độ truyền âm trong ống.
Phương pháp giải: Quan sát đồ thị hiện trên màn hình để xác định chu kì. Tính tần số sóng f=1T. Sự thay đổi chiều dài ống cộng hưởng giữa hai lần liên tiếp nghe được âm thanh rất to là khoảng cách giữa hai bụng sóng. Xác định tốc độ truyền âm bằng công thức v=fλ. Lời giải chi tiết: a) Từ hình vẽ, ta thấy một chu kì sóng tương ứng với 2,25 độ chia, do đó chu kì sóng là: T=2,25.(1,0.10−3)=2,25.10−3(s) . Tần số sóng là : f=1T=12,25.10−3=40009≈444,4(Hz). b) Giữa hai lần liên tiếp nghe được âm rất to tại miệng ống (miệng ống là bụng sóng), chiều dài ống cộng hưởng đã thay đổi một khoảng d=λ2, do đó, bước sóng là: λ=2d=2.0,32=0,64(m). Tốc độ truyền âm trong ống là: v=fλ=8009.1,98=176(m/s).
|