Bài 21. Moment lực. Cân bằng của vật rắn trang 37, 38, 39 SBT Vật lí 10 Kết nối tri thức với cuộc sốngTrường hợp nào sau đây, lực có tác dụng làm cho vật rắn quay quanh trục? Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Lựa chọn câu để xem lời giải nhanh hơn
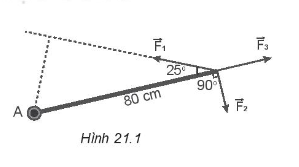
21.1 Trường hợp nào sau đây, lực có tác dụng làm cho vật rắn quay quanh trục? A. Lực có giá song song với trục quay. B. Lực có giá cắt trục quay. C. Lực có giá nằm trong mặt phẳng vuông góc với trục quay và cắt trục quay. D. Lực có giá nằm trong mặt phẳng vuông góc với trục quay và không cắt trục quay. Phương pháp giải: Vận dụng moment lực. Lời giải chi tiết: Moment lực đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực và được đo bằng tích của lực với cánh tay đòn của nó: M = F.d Trong đó cánh tay đòn d của lực →Flà khoảng cách từ trục quay đến giá của lực. Các trường hợp lực có giá song song với trục quay hay có giá cắt trục quay à cánh tay đòn bằng 0 à moment của lực F đối với trục quay bằng 0 không làm cho vật quay quanh trục. Lực có giá nằm trong mặt phẳng vuông góc với trục quay và không cắt trục quay → cánh tay đòn khác không → moment của lực F đối với trục quay khác không sẽ làm cho vật quay quanh trục quay. Chọn đáp án D. 21.2 Biết F1 = 25 N, F2 = 10 N, F3 = 10 N. Moment của các lực trong Hình 21.1: M(F1); M(F2); M(F3) đối với trục quay A lần lượt là
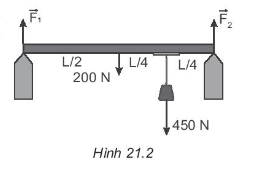
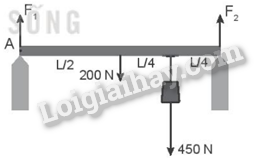
A. - 8 N.m; 8,5 N.m; 0. B. -0,8 N.m; 8,5 N.m; 0. C. 8 N.m; 8,5 N.m; 0. D. 8,5 N.m; -8 N.m; 0. Phương pháp giải: Vận dụng công thức tính moment lực: M = F.d. Lời giải chi tiết: Chọn chiều dương là chiều ngược chiều quay của kim đồng hồ. Áp dụng công thức: M = F.d. Ta có: M(F1) = F1.d1 = 25.0,8.sin25o ≈ 8,5 N.m. M(F2) = F2.d2= - 10.0,8 = - 8 N.m. M(F3) = F3.d3 = - 10.0 = 0 N.m Chọn đáp án D. 21.3 Một thanh đồng chất có chiều dài L, trọng lượng 200 N, treo một vật có trọng lượng 450 N vào thanh như Hình 21.2. Các lực →F1,→F2của thanh tác dụng lên hai điểm tựa có độ lớn lần lượt là
A. 212 N; 438 N. B. 325 N; 325 N. C. 438 N; 212 N. D. 487,5 N; 162,5 N. Phương pháp giải: Sử dụng điều kiện cân bằng tổng quát của vật rắn. + Tổng các lực tác dựng lên vật bằng 0. + Tổng các moment lực tác dụng lên vật đối với một điểm bất kì bằng 0 (nếu chọn một chiều quay làm chiều dương). Lời giải chi tiết:
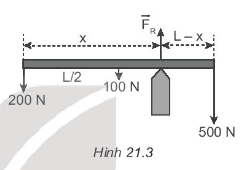
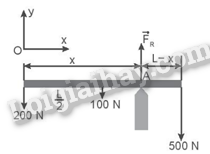
Chọn chiều (+) thẳng đứng hướng lên trên. Các lực thành phần theo phương Oy cân bằng nhau như hình vẽ: F1 + F2 – 200 – 450 = 0 Áp dụng quy tắc momen lực đối với trục quay tại A: F1d1 – P1d2 – P2d3 + F2d4 = 0 => L2.200+3L4450=LF2 => F2 = 437,5 N ≈ 438 N => F1 = 212 N. Chọn đáp án A. 21.4 Một đường ống đồng chất có trọng lượng 100 N, chiều dài L, tựa trên điểm tựa như Hình 21.3. Khoảng cách x và phản lực FR của điểm tựa tác dụng lên đường ống là
A. x = 0,69L; FR = 800 N. B. x = 0,69L; FR = 400 N. C. x = 0,6L; FR = 552 N. D. x = 0,6L; FR =248 N. Phương pháp giải: Sử dụng điều kiện cân bằng tổng quát của vật rắn. + Tổng các lực tác dựng lên vật bằng 0. + Tổng các moment lực tác dụng lên vật đối với một điểm bất kì bằng 0 (nếu chọn một chiều quay làm chiều dương). Lời giải chi tiết:
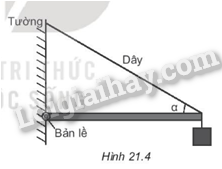
Chọn hệ trục tọa độ Oxy có chiều dương như hình vẽ. Các lực thành phần theo phương Oy cân bằng nhau như hình vẽ: FR – 200 – 100 – 500 = 0. => FR = 800 N. Áp dụng quy tắc moment lực đối đối với trục quay tại A: x.200+(x−L2).100−(L−x).500=0. => 800x = 550L => x = 0,69L. Chọn đáp án A. 21.5 Một thanh có độ dài L, trọng lượng 10 N, được treo nằm ngang vào tường như Hình 21.4. Một trọng vật 20 N treo ở đầu thanh. Dây treo làm với thanh một góc α = 30°. Xác định lực căng của dây treo.
Phương pháp giải: Áp dụng điều kiện cân bằng tổng quát của vật rắn. + Tổng các lực tác dựng lên vật bằng 0. + Tổng các moment lực tác dụng lên vật đối với một điểm bất kì bằng 0 (nếu chọn một chiều quay làm chiều dương). Lời giải chi tiết:
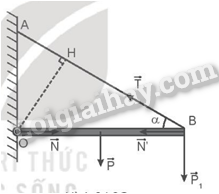
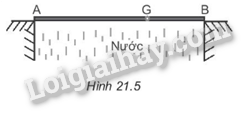
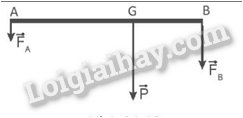
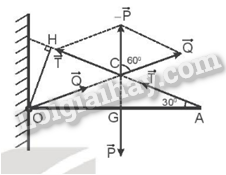
Thanh chịu tác dụng của các lực được biểu diễn như hình vẽ. Áp dụng điều kiện cân bằng đối với trục quay tại O, ta có: 0.N + OH.T = L2.P + LP1 => Lsinα.T = L2.P + LP1 => T = P2+P1sinα= 5+20sin30o= 50 N. Vậy lực căng của dây treo là 50 N. 21.6 Một tấm ván nặng 150 N được bắc qua một con mương. Biết trọng tâm G của tấm ván cách điểm tựa A một khoảng là 2 m và cách điểm tựa B một khoảng 1 m (Hình 21.5). Hãy xác định lực mà tấm ván tác dụng lên hai bờ mương.
Phương pháp giải: Sử dụng điều kiện cân bằng tổng quát của vật rắn. + Tổng các lực tác dựng lên vật bằng 0. + Tổng các moment lực tác dụng lên vật đối với một điểm bất kì bằng 0 (nếu chọn một chiều quay làm chiều dương). Áp dụng biểu thức moment lực: M = Fd. Lời giải chi tiết:
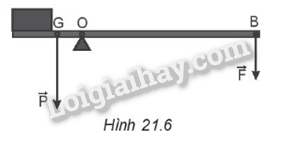
Hai đầu của tấm ván tác dụng lên hai bờ mương là →FA,→FB. Vì tấm ván được đặt cân bằng nên ta có: FA + FB = 150 N (1) Và: M(FA) = M(FB) => FA.GA = FB. GB => FAFB=GBGA=12 (2) Từ (1), (2) giải hệ phương trình ta tìm được: FA = 50 N; FB = 100 N. 21.7 Một thanh chắn đường dài 8 m, có trọng lượng 220 N và có trọng tâm cách đầu bên trái 1,5 m (Hình 21.6). Thanh có thể quay quanh một trục nằm ngang ở cách đầu bên trái 1,8 m. Để giữ thanh cân bằng thì phải tác dụng vào đầu bên phải một lực bằng bao nhiêu?
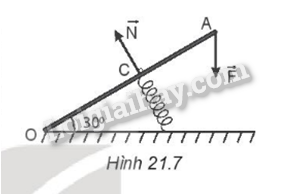
Phương pháp giải: Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ. Áp dụng quy tắc moment lực: ∑M=0 Trong đó biểu thức moment lực: M = Fd. Lời giải chi tiết: Thanh chắn là vật rắn có trục quay cố định (O) cân bằng dưới tác dụng của 2 lực gây momen →Pvà →F. Chọn chiều (+) là chiều kim đồng hồ. Áp dụng quy tắc moment lực: ∑M=0=> M(P) + M(F) = 0 => P.OG – F.OB = 0 => P.OG = F.OB => F = P.OGOB Với OG = 1,8 – 1,5 = 0,3 m; OB = 8 – 1,8 = 6,2 m. => F = 220.0,36,2≈ 10,6 N. 21.8 Một thanh OA có khối lượng không đáng kể, chiều dài 30 cm, có thể quay dễ dàng quanh trục nằm ngang O. Gắn vào điểm giữa C một lò xo. Người ta tác dụng vào đầu A một lực F = 20 N hướng thẳng đứng xuống dưới (Hình 21.7). Khi thanh ở trạng thái cân bằng lò xo có phương vuông góc với OA và OA hợp với phương nằm ngang một góc 30°. a) Xác định độ lớn phản lực N của lò xo vào thanh. b) Tính độ cứng k của lò xo, biết lò xo bị nén lại 10 cm so với ban đầu.
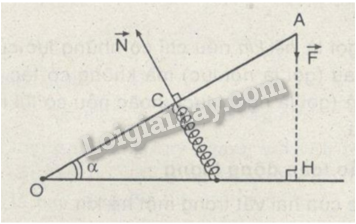
Phương pháp giải: a) Áp dụng quy tắc moment lực: M(N) = M(F) Trong đó biểu thức moment lực: M = Fd. b) Áp dụng định luật Húc: Fđh = k.∆l. Lời giải chi tiết:
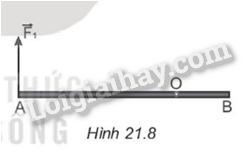
a) Ta có: OA = 30 cm; OC = OA2= 15 cm; F = 20 N; α = 30o => OH = OA.cosα = 30.cos30o = 15√3 cm. Thanh OA là vật rắn có trục quay (O) cân bằng dưới tác dụng của hai lực có momen lực →Fcó tay đòn OH; phản lực →Ncó tay đòn OC. Áp dụng quy tắc momen ta có: N.OC = F.OH => N = F.OHOC= 20.15√315= 20√3 ≈ 34,6 N. b) Theo định luật III Newton ta có: Fdh = N = 20√3. Áp dụng định luật Húc: Fđh = k.∆l => k = NΔl= 20√30,1 ≈ 346 N/m. 21.9 Một cái thước AB = 1,2 m đặt trên mặt bàn nhẵn nằm ngang, có trục quay O cách đầu A một khoảng 80 cm (Hình 21.8). Một lực F1 = 5 N tác dụng lên đầu A theo phương vuông góc với thước và lực thứ hai tác dụng lên đầu B của thước theo phương vuông góc với thước (không vẽ trên hình). Các lực đều nằm trên mặt phẳng nằm ngang. Nếu thước không chuyển động thì lực tác dụng vào đầu B của thước có hướng và độ lớn như thế nào?
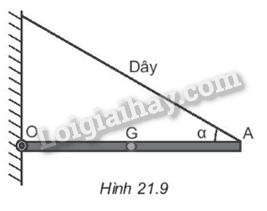
Phương pháp giải: Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ. Áp dụng quy tắc moment lực: ∑M=0 Trong đó biểu thức moment lực: M = Fd. Lời giải chi tiết: OA = 80 cm = 0,8 m; OB = AB – OA = 1,2 – 0,8 = 0,4 m. Muốn cho một vật có trục quay cố định ở trạng thái cân bằng, thì tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ. Chọn chiều (+) là chiều kim đồng hồ. Ta có 2 lực ở 2 bên so với trục quay. Thước không chuyển động nên: Áp dụng quy tắc moment lực: ∑M=0 => M(F1) = M(F2) => F1.OA = F2.OB => F2 = F1.OAOB= 5.0,80,4= 10 N. Vậy F2 = 10 N, →F2cùng hướng →F1 21.10 Một thanh dài AO, đồng chất, có khối lượng 1,2 kg. Một đầu O của thanh liên kết với tường bằng một bản lề, còn đầu A được treo vào tường bằng một sợi dây AB. Thanh được giữ nằm ngang và dây làm với thanh một góc α = 30° (Hình 21.9). Lấy g = 10 m/s2. Tính lực căng của dây.
Phương pháp giải: Áp dụng quy tắc moment lực: ∑M=0 Trong đó biểu thức moment lực: M = Fd. Lời giải chi tiết:
Thanh có trục quay cố định O, chịu tác dụng của ba lực →P, →T và →Q. Áp dụng quy tắc moment lực, ta được: ∑M=0 => M(O)T=M(O)P (M(O)Q = 0) => T.OH = P.OG => T.12.OA = P. 12.OA => T = P = mg = 1,2.10 = 12 N.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|