Bài 2. Phương trình trạng thái khí lí tưởng trang 23, 24, 25 SBT Vật lí 12 Cánh diều

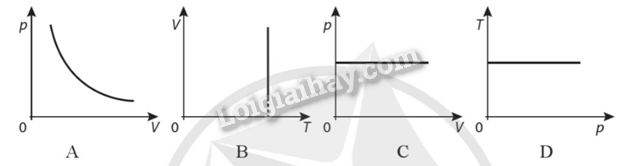
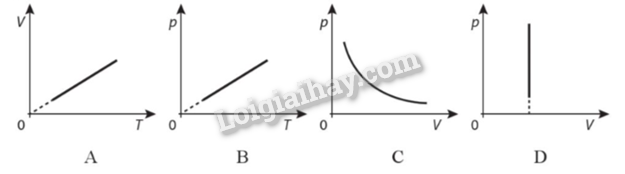
2.7

Hình nào sau đây không phải là đồ thị biểu diễn quá trình đẳng nhiệt?

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng nhiệt

Lời giải chi tiết:

Hình C là quá trình đẳng tích

Đáp án: C

2.8

Đâu là nhóm các thông số trạng thái của một lượng khí xác định?

A. Áp suất, nhiệt độ, thể tích.

B. Áp suất, nhiệt độ, khối lượng.

C. Khối lượng, nhiệt độ, thể tích.

D. Khối lượng, áp suất, thể tích.

Phương pháp giải:

Vận dụng lý thuyết về trạng thái của một lượng khí xác định

Lời giải chi tiết:

Trạng thái của một lượng khí xác định bao gồm: áp suất, nhiệt độ, thể tích.

Đáp án: A

2.9

Hệ thức nào sau đây thể hiện đúng mối liên hệ giữa các thông số trạng thái khí lí tưởng trong quá trình đẳng áp?

A. \({p_1}{V_1} = {p_2}{V_2}\)

B. \(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}}\)

C.\({V_1}{T_1} = {V_2}{T_2}\)

D. \(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}}\)

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng áp

Lời giải chi tiết:

Mối liên hệ giữa các thông số trạng thái khí lí tưởng trong quá trình đẳng áp là: \(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}}\)

Đáp án: B

2.10

Đồ thị nào sau đây biểu diễn quá trình biến đổi trạng thái của khí lí tưởng khi áp suất không đổi?

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng áp

Lời giải chi tiết:

Hình A là quá trình đẳng áp

Đáp án: A

2.11

Trong quá trình nào sau đây, cả ba thông số trạng thái p, V, T của một lượng khí xác định đều thay đổi?

A. Không khí được nung nóng trong một bình đậy kín.

B. Không khí trong một phòng mở cửa khi nhiệt độ môi trường và áp suất khí quyển tăng lên.

C. Khi nitrogen trong quả bóng bay bị bóp xẹp từ từ.

D. Khí oxygen trong bình kín vừa được làm lạnh vừa được nén cho áp suất không đổi.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng áp

Lời giải chi tiết:

Không khí trong một phòng mở cửa khi nhiệt độ môi trường và áp suất khí quyển tăng lên làm cả ba thông số trạng thái p, V, T đều thay đổi

Đáp án: B

2.12

Một lượng khí ở nhiệt độ 30 °C có thể tích 1,0 m³ và áp suất 2,0.10⁵ Pa. Thực hiện nén khí đẳng nhiệt đến áp suất 3,5.10⁵ Pa thì thể tích của lượng khí là

A. 0,6.10⁵ m³.

B. 1,75 m³.

C. 0,6.10^-5 m³.

D. 0,6 m³.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng nhiệt

Lời giải chi tiết:

\({p_1}{V_1} = {p_2}{V_2} \to {V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{{{2.10}^5}.1}}{{{{3,5.10}^5}}} = \frac{4}{7} \approx 0,6({m^3})\)

Đáp án: D

2.13

Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai?

a) Một lượng khí được xác định bởi số các phân tử khí.

b) Đường đẳng nhiệt trong hệ toạ độ (p – T) là đường hypebol.

c) Định luật Boyle cho biết mối liên hệ tỉ lệ thuận giữa áp suất và thể tích của một lượng khí xác định khi nhiệt độ không đổi.

d) Định luật Boyle cho biết mối liên hệ tỉ lệ nghịch giữa áp suất và thể tích của một lượng khí xác định khi nhiệt độ không đổi.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

a) Đúng

b) Sai. Đường đẳng nhiệt trong hệ toạ độ (p – T) là đường thẳng

c) Sai. Định luật Boyle cho biết mối liên hệ tỉ lệ nghịch giữa áp suất và thể tích của một lượng khí xác định khi nhiệt độ không đổi.

d) Đúng

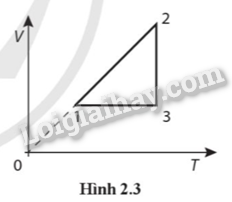
2.14

Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai?

a) Định luật Charles là định luật thu được từ kết quả thực nghiệm về chất khí.

b) Đường biểu diễn quá trình đẳng áp của một lượng khí trong hệ toạ độ (V-T) là đường thẳng kéo dài đi qua gốc toạ độ.

c) Trong quá trình đẳng áp, thể tích của một lượng khi luôn tỉ lệ nghịch với nhiệt độ (K) của lượng khi đó.

d) Phương trình trạng thái của khí lí tưởng thể hiện mối liên hệ giữa nhiệt độ, khối lượng và áp suất của một lượng khí.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

a) Đúng

b) Đúng

c) Sai. Trong quá trình đẳng áp, thể tích của một lượng khi luôn tỉ lệ thuận với nhiệt độ (K) của lượng khi đó.

d) Sai. Phương trình trạng thái của khí lí tưởng thể hiện mối liên hệ giữa nhiệt độ, thể tích và áp suất của một lượng khí.

2.15

Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai?

a) Khi thể tích được giữ không đổi, áp suất của một lượng khí tỉ lệ nghịch với

nhiệt độ.

b) Với một lượng khí lí tưởng thì \(\frac{{pV}}{T}\)là hằng số.

c) Khi nhiệt độ tăng từ 20 °C lên 40 °C thì áp suất của một lượng khí trong bình kín sẽ tăng lên hai lần.

d) Đường biểu diễn quá trình đẳng tích (thể tích không đổi) của một lượng khí trong hệ toạ độ (p - T) là đường thẳng kéo dài đi qua gốc toạ độ.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

a) Sai. Khi thể tích được giữ không đổi, áp suất của một lượng khí tỉ lệ thuận với

nhiệt độ.

b) Đúng

c) Sai. Khi nhiệt độ tăng từ 20 °C lên 40 °C \( \Leftrightarrow \) t₁ = 293 K; t₂ = 313 K thì áp suất của một lượng khí trong bình kín sẽ tăng lên 1,07 lần.

d) Đúng

2.16

Buồng chứa sản phẩm điều chế là khí hydrogen được giữ ở 20,0 °C và áp suất 1,00 atm. Cần lấy ..... m³ khí hydrogen từ buồng này để nạp đầy bình có thể tích 0,0500 m³ và áp suất 25,0 atm. Coi quá trình nạp khí được giữ cho nhiệt độ không đổi.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng nhiệt

Lời giải chi tiết:

Áp dụng định luật Boyle, ta có:

\({p_1}{V_1} = {p_2}{V_2} \Leftrightarrow {V_1} = \frac{{{p_2}{V_2}}}{{{p_1}}} = \frac{{25.0,05}}{1} = 1,25({m^3})\)

2.17

Một bình chứa oxygen ở điều kiện bảo quản 20,0 °C thì có áp suất 5,0 atm. Nếu nhiệt độ phòng bảo quản tăng lên 40,0 °C thì áp suất của bình là ....atm

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng tích

Lời giải chi tiết:

Áp dụng định luật Sác-lơ, ta có:

\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \Leftrightarrow {p_2} = \frac{{{p_1}{T_2}}}{{{T_1}}} = \frac{{5.313}}{{293}} \approx 5,34(atm)\)

2.18

Một bình chứa khí có vách ngăn di chuyển được. Khi dịch vách ngăn để bình có thể tích 15,0 lít ở nhiệt độ 27,0 °C thì áp suất khí trong bình là 1,50 atm. Tiếp tục dịch chuyển vách ngăn để nén khi đến thể tích 12,0 lít thì áp suất khí trong bình là 3,00 atm. Nhiệt độ của khí trong bình lúc này là ...... C.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Leftrightarrow {T_2} = \frac{{{p_2}{V_2}{T_1}}}{{{p_1}{V_1}}} = \frac{{3.12.300}}{{1,5.15}} = 480(K) = 207{(^o}C)\)

2.19

Ở điều kiện tiêu chuẩn (nhiệt độ 0 °C và áp suất 1,00 atm) thì khí oxygen có khối lượng riêng là 1,43 kg/m . Tính khối lượng khí oxygen gây ra áp suất 25,0 atm trong bình chứa 10,0 lít ở 0 °C.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

Áp dụng định luật Boyle, ta có:

\({p_1}{V_1} = {p_2}{V_2} \Leftrightarrow {V_1} = \frac{{{p_2}{V_2}}}{{{p_1}}} = \frac{{25.10}}{1} = 250(l) = {250.10^{ - 3}}({m^3})\)

Khối lượng khí oxygen gây ra áp suất 25 atm trong bình chứa 10 lít ở 0 °C là:

m = pV₁ = 1,43.250.10^-3 = 0,3575 = 35,75.10^-2 (kg)

2.20

Để mở nút chai bị kẹt, một người dùng cách hơ nóng khí trong chai. Biết rằng khí trong chai lúc chưa hơ nóng thì có áp suất bằng áp suất khí quyển 1,0.10⁵ Pa và

có nhiệt độ là 7 °C. Để làm nút bật ra cần có chênh lệch áp suất giữa khí trong chai và bên ngoài là 0,6.10⁵ Pa. Người này cần làm khí trong chai nóng đến nhiệt độ ít nhất bằng bao nhiêu để nút chai bật ra?

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng tích

Lời giải chi tiết:

Áp dụng định luật Sác-lơ, ta có:

\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \Leftrightarrow {T_2} = \frac{{{p_2}{T_2}}}{{{p_1}}} = \frac{{{{1,6.10}^5}.280}}{{{{1.10}^5}}} = 448(K)\)

2.21

Một mol khí lí tưởng có các quá trình biến đổi. giữa ba trạng thái 1, 2, 3 được biểu diễn trong hệ toạ độ thể tích V (m³) - nhiệt độ T (K) như đồ thị Hình 2.3. Hãy vẽ đồ thị biểu diễn các quá trình này của mol khí trong hệ toạ độ áp suất p (Pa) - nhiệt độ T (K).

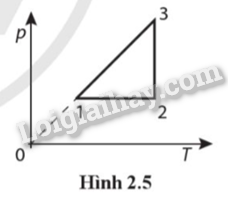
Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

Mol khí có quá trình 1 → 2 là đẳng áp, 2 → 3 là đẳng nhiệt, 3 → 1 là đẳng tích được biểu diễn trong hệ toạ độ (p − T) như Hình 2.5.

2.22

Bóng thám không là một thiết bị thường dùng trong ngành khí tượng để hỗ trợ thu thập các thông số của các tầng khí quyển. Một bóng thám không ở dưới mặt đất được bơm khí ở áp suất 1,00 atm và nhiệt độ 27 °C. Để bóng này khi lên đến tầng khí quyển có áp suất 0,04 atm và nhiệt độ  −50 °C vẫn không phình quá 5,00.10² m³ thì thể tích bóng khi được bơm ở mặt đất tối đa là bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Leftrightarrow {V_1} = \frac{{{p_2}{V_2}{T_1}}}{{{p_1}{T_2}}} = \frac{{{{0,04.5.10}^2}.300}}{{1.223}} = 26,9({m^3})\)

2.23

Một phòng trống có kích thước 5,0 m × 10,0 m × 3,0 m. Lúc đầu, không khí trong phòng ở điều kiện tiêu chuẩn (nhiệt độ 0,0 °C và áp suất 1,0.10⁵ Pa) và có khối lượng mol là 29 g/mol.

a) Xác định số mol và khối lượng không khí có trong phòng. Biết hằng số khí lí tưởng là R = 8,31 J.mol^-1 K^-1

b) Khi mở cửa phòng thì nhiệt độ phòng tăng lên 20 °C và áp suất khí trong phòng bằng áp suất bên ngoài phòng là 0,9.10⁵ Pa. Tính khối lượng không khí trong phòng đã thoát ra ngoài.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

a) pV = nRT → số mol không khí trong phòng là n = 6,6.10³ mol.

Khối lượng không khí trong phòng là m = 1,9.10² g.

b) Xét lượng khí trong phòng lúc đầu khi ở nhiệt độ 20 °C và áp suất 0,9.10⁵ Pa có thể tích là V₂ = 178 m³ lớn hơn thể tích phòng V₁ = 150 m³. Như vậy, đã có ∆V = 28 m³ khí ở nhiệt độ 20 °C và áp suất 0,9.10⁵ Pa thoát ra khỏi phòng.

Khối lượng không khí trong phỏng đã thoát ra ngoài bằng:

\(\Delta m = \frac{{28}}{{178}}m = \frac{{14}}{{89}}({1,9.10^2}) = {0,3.10^2}(g)\)

2.24

Một người chế tạo dụng cụ đo độ nghiêng của bề mặt nằm ngang là một ống thuỷ tinh tiết diện S nhỏ được bịt kín hai đầu. Trong ống có chứa khí và ở giữa ống có một cột thuỷ ngân (Hg) dài l. Khi đặt ống trên mặt phẳng nằm ngang, cột thuỷ ngân nằm chính giữa ống (Hình 2.4a) và phần ống chứa khí ở hai đầu dài L như nhau. Khi dựng ống thẳng đứng, cột thuỷ ngân bị dịch xuống một đoạn ∆l, phần ống chứa khí phía dưới ngắn hơn phần ống phía trên (Hình 2.4b).

a) Vì sao cột thuỷ ngân lại dịch xuống khi dựng ống thẳng đứng?

b) Cho L = 0,50 m; l = 0,10 m; ∆l = 0,05 m. Hãy xác định áp suất p_o của khí trong ống thuỷ tinh khi ống nằm ngang theo đơn vị cmHg.

Phương pháp giải:

Vận dụng kiến thức về quá trình đẳng khí

Lời giải chi tiết:

a) Khi ống thuỷ tinh nằm ngang, phần ống chứa khí ở hai đầu dài bằng nhau nên lượng khí ở hai đầu ống là giống nhau, có thể xem như cùng một lượng khí. Khi dựng ống thuỷ tinh thẳng đứng, áp suất của cột khí phía dưới p₁ cân bằng với áp suất của cột khí phía trên p₂ và áp suất của cột thuỷ ngân p_Hg : p₁ = p₂ + p_Hg hay

p₁ > p₂.

Do đó, cột thuỷ ngân dịch xuống để thể tích phần khí phía dưới nhỏ hơn thể tích khí phía trên.

b) \({p_2} = \frac{{{p_{Hg}}(L - \Delta l)}}{{2\Delta l}} = 45(cmHg)\)

Áp dụng định luật Boyle cho lượng khí ở phần ống phía trên:

– Khi ống nằm ngang, lượng khí này có áp suất p_o và thể tích SL.

– Khi ống thẳng đứng, lượng khí này có áp suất p₂ và thể tích S(L + ∆l).

Vậy p_o = 49,5 cmHg.