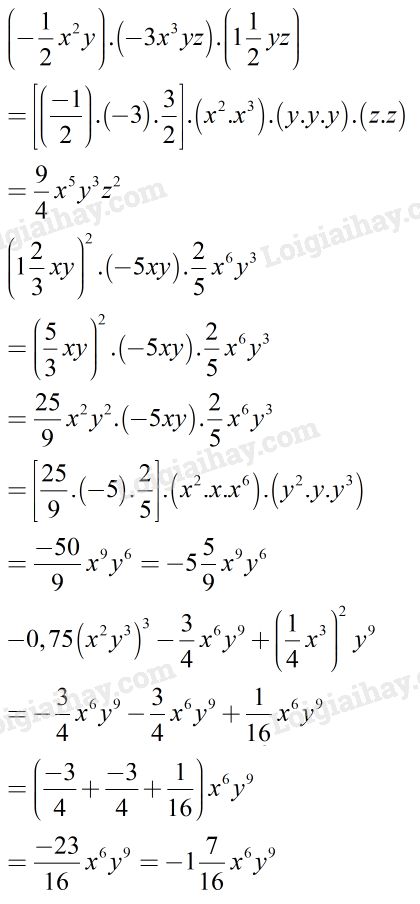Phần câu hỏi bài 4 trang 36, 37 Vở bài tập toán 7 tập 2Giải phần câu hỏi bài 4 trang 36, 37 VBT toán 7 tập 2. Nối một biểu thức ở cột bên phải với một biểu thức ở cột bên trái để được hai đơn thức đồng dạng...
Lựa chọn câu để xem lời giải nhanh hơn
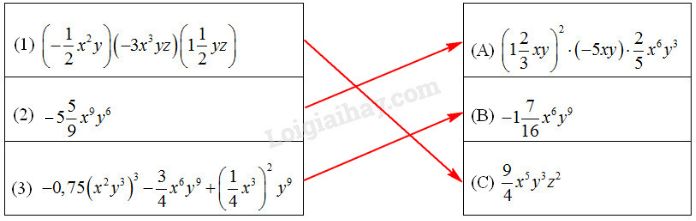
Câu 10. Nối một biểu thức ở cột bên phải với một biểu thức ở cột bên trái để được hai đơn thức đồng dạng
Phương pháp giải: - Muốn cộng hoặc trừ các đơn thức đồng dạng, ta cộng hoặc trừ các hệ số với nhau và giữ nguyên phần biến. Lời giải chi tiết:
Ta nối như sau:
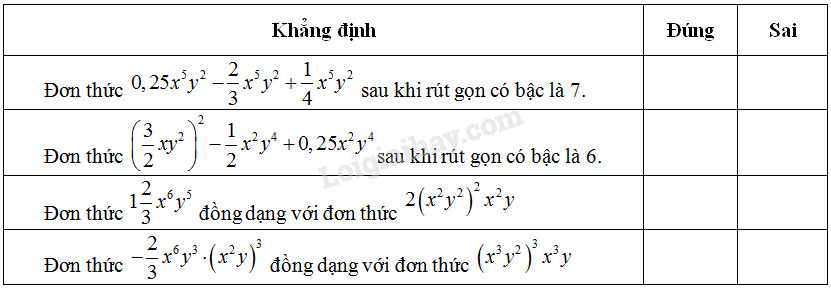
Chú ý: Sửa đề bài 559x9y6⇒−559x9y6 để bài toán có lời giải phù hợp. Câu 11. Điền “×” vào ô trống trong bảng sau
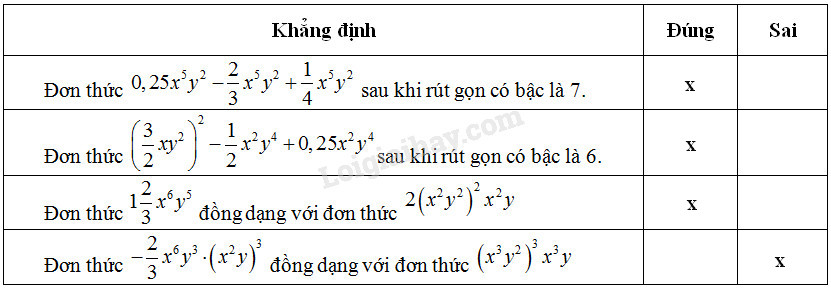
Phương pháp giải: - Muốn cộng hoặc trừ các đơn thức đồng dạng, ta cộng hoặc trừ các hệ số với nhau và giữ nguyên phần biến. - Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó. Lời giải chi tiết: Ta điền như sau:
Giải thích: 0,25x5y2−23x5y2+14x5y2=(14−23+14)x5y2=−16x5y2 Đơn thức sau khi rút gọn có bậc là 7. (32xy2)2−12x2y4+0,25x2y4=94x2y4−12x2y4+14x2y4=(94−12+14)x2y4=2x2y4 Đơn thức sau khi rút gọn có bậc là 6. 2(x2y2)2x2y=2x4y4.x2y=2x6y5 Do đó đơn thức 123x6y5 đồng dạng với đơn thức 2(x2y2)2x2y −23x6y3(x2y)3=−23x6y3.x6y3=−23x12y6 (x3y2)3x3y=x9y6.x3y=x12y7 Do đó đơn thức −23x6y3(x2y)3 không đồng dạng với (x3y2)3x3y. Câu 12. Khoanh tròn vào chữ cái trước khẳng định đúng Hệ số của đơn thức (sau khi rút gọn) (A) x5y3−12(x2y)2xy+(−23x5y)(−y)2 là −16; (B) x6y3z4−32(x3yz2)2y+(−x2yz)3 là −0,5; (C) −25(ab)2a2−35ab(a3b)3+(112a2b)2 là 1,5; (D) (−a2bc2)3−35(−a2b)3c6 là 25. Phương pháp giải: - Rút gọn đơn thức. - Tìm hệ số rồi chọn đáp án. Lời giải chi tiết: Xét đáp án A: x5y3−12(x2y)2xy+(−23x5y)(−y)2 =x5y3−12x5y3+(−23)x5y3 =(1−12−23)x5y3=−16x5y3 Đơn thức thu được có hệ số là −16 nên A đúng. Chọn A. HocTot.Nam.Name.Vn
|