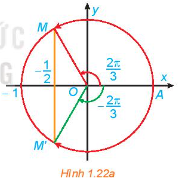
Giải mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức

HĐ 3

a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng $\left[ { - \pi ;\pi } \right)$.

b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.

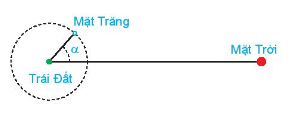
Phương pháp giải:

Nghiệm của phương trình $\cos x =  - \frac{1}{2}$ là hoành độ các giao điểm của đường thẳng $y =  - \;\frac{1}{2}$ và đồ thị hàm số $y = \cos x$

Lời giải chi tiết:

a) Từ Hình 1.20, ta thấy đường thẳng $y = \frac{1}{2}$ cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: $\frac{\pi }{6}, - \frac{{5\pi }}{6}$

b) Vì hàm số $\cos x$ tuần hoàn với chu kỳ là $2\pi$, ta có công thức nghiệm của phương trình là: $\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi  - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.$

Quảng cáo

LT 3

Giải các phương trình sau:

a) $2\cos x =  - \sqrt 2$;            b) $\cos 3x - \sin 5x = 0$

Phương pháp giải:

Dựa vào công thức nghiệm tổng quát:

$\cos x = m\;\; \Leftrightarrow \cos x = \cos \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha  + k2\pi }\\{x =  - \alpha  + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;$

Lời giải chi tiết:

a) $2\cos x =  - \sqrt 2  \Leftrightarrow \cos x =  - \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \cos x = \cos \frac{\pi }{4} \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi  - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.$

b) $\cos 3x - \sin 5x = 0\;\;\;\; \Leftrightarrow \cos 3x = \sin 5x\;\;\;\; \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} - 5x} \right)\;\;$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \frac{\pi }{2} - 5x + k2\pi }\\{3x =  - \frac{\pi }{2} + 5x + k2\pi }\end{array}} \right.\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{8x = \frac{\pi }{2} + k2\pi }\\{ - 2x =  - \frac{\pi }{2} + k2\pi }\end{array}} \right.\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{\pi }{4} - k\pi }\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)$

VD

Khi mặt trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là $\alpha \left( {{0^0} \le \;\alpha  \le {{360}^0}} \right)$thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bới công thức:

$F = \frac{1}{2}\left( {1 - \cos \alpha } \right)$.

Xác định góc $\alpha$ tương ứng với các pha sau của Mặt Trăng.

a) $F = 0$ (trăng mới)

b) $F = 0,25$ (trăng lưỡi liềm)

c) $F = 0,5$ (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)

d) $F = 1$ (trăng tròn)

Phương pháp giải:

Thay giá trị F tương ứng rồi giải phương trình để tìm $\alpha$

Lời giải chi tiết:

a)

$\begin{array}{l}F = 0\;\\ \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0\;\; \Leftrightarrow 1 - \cos \alpha  = 0\;\; \Leftrightarrow \cos \alpha  = 1\; \Leftrightarrow \alpha  = k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array}$

b) $F = 0,25\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,25\; \Leftrightarrow 1 - \cos \alpha  = \frac{1}{2}\;\; \Leftrightarrow \cos \alpha  = \frac{1}{2}\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha  = \frac{\pi }{3} + k2\pi }\\{\alpha  =  - \frac{\pi }{3} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.$

c) $F = 0,5\;\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,5\; \Leftrightarrow 1 - \cos \alpha  = 1\; \Leftrightarrow \cos \alpha  = 0\; \Leftrightarrow \alpha  = \frac{\pi }{2} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)$

d) $F = 1\; \Leftrightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 1\;\; \Leftrightarrow 1 - \cos \alpha  = 2\; \Leftrightarrow \cos \alpha  =  - 1\; \Leftrightarrow \alpha  = \pi  + k2\pi \;\left( {k \in \mathbb{Z}} \right)$