Giải mục 2 trang 72, 73, 74 SGK Toán 11 tập 1 - Kết nối tri thứcChiếc xà ngang đặt tựa lên hai điểm A, B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi qua hai điểm đó. Có thể tìm được một đường thẳng khác cũng đi qua hai điểm A,B hay không? Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
HĐ 2 Video hướng dẫn giải - Chiếc xà ngang đặt tựa lên hai điểm A, B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi qua hai điểm đó. Có thể tìm được một đường thẳng khác cũng đi qua hai điểm A,B hay không?
- Câu hỏi: Có bao nhiêu đường thẳng đi qua hai trong số ba điểm không thẳng hàng? Phương pháp giải: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt. Lời giải chi tiết: - Không thể tìm được đường thẳng khác đi qua hai điểm A,B. - Trả lời câu hỏi: Với mỗi 2 điểm phân biệt sẽ có duy nhất một đường thẳng đi qua. Như vậy, với 3 điểm không thẳng hàng sẽ tạo thành 3 cặp điểm phân biệt nên sẽ có 3 đường thẳng đi qua 2 trong số 3 điểm đó HĐ 3 Video hướng dẫn giải - Trong Hình 4.4 là một khối rubik có bốn đỉnh và bốn mặt, mỗi mặt là một tam giác. a) Đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn. Khi đó, mặt màu đỏ của khối rubik có nằm trên mặt bàn hay không? b) Có thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn hay không?
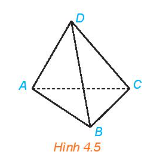
- Câu hỏi: Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng? Phương pháp giải: - Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. - Tồn tại bốn điểm không cùng thuộc một mặt phẳng. Lời giải chi tiết: a) Vì 3 đỉnh của mặt màu đỏ đều nằm trên mặt bàn nên mặt màu đỏ cũng nằm trên mặt bàn. b) Không thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn vì bốn đỉnh của rubik không cùng thuộc một mặt phẳng. Trả lời câu hỏi: Có vô số mặt phẳng đi qua ba điểm thẳng hàng LT 1 Video hướng dẫn giải Cho tứ giác ABCD. Có bao nhiêu mặt phẳng đi qua ba trong số bốn đỉnh của tứ giác đó?
Phương pháp giải: Một mặt phẳng hoàn toàn xác định nếu biết ba điểm không thẳng hàng thuộc mặt phẳng đó. Lời giải chi tiết: Có 4 mặt phẳng đi qua ba trong số bốn đỉnh của tứ giác đó là: (DAB), (DAC), (DBC), (ABC). VD 1 Video hướng dẫn giải Hãy giải thích tại sao trong thực tiễn có nhiều đồ vật được thiết kế gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nồi,… Phương pháp giải: Dựa vào các tính chất thừa nhận của mặt phẳng. Lời giải chi tiết: Với thiết kế 3 chân, tạo thành mặt phẳng cố định giúp giá đỡ được chắc chắn hơn. HĐ 4 Video hướng dẫn giải Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. Khi đó, sợi dây nằm trên mặt bàn hay không? Phương pháp giải: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó. Lời giải chi tiết: Vì hai đầu của sợi dây là hai điểm thuộc sợi dây đó nằm trên mặt bàn nên sợi dây đó cũng nằm trên mặt bàn. LT 2 Video hướng dẫn giải Trong Ví dụ 2, lấy điểm N thuộc đường thẳng AB sao cho N khác M. Đường thẳng MN có thuộc mặt phẳng (ABC) hay không? Phương pháp giải: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó. Lời giải chi tiết: Đưởng thẳng MN có hai điểm phân biệt M, N thuộc mặt phẳng (ABC) nên đường thẳng MN nằm trong mặt phẳng (ABC).
HĐ 5 Video hướng dẫn giải Trong Hình 4.7, mặt nước và thành bể có giao nhau theo đường thẳng hay không?
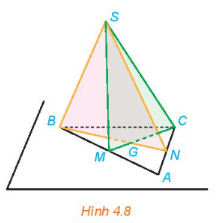
Phương pháp giải: Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Lời giải chi tiết: Mặt nước và thành bể có giao nhau theo đường thẳng đi qua các điểm chung. LT 3 Video hướng dẫn giải Trong Ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN). Phương pháp giải: Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung thuộc cả hai mặt phẳng đó. Lời giải chi tiết:
Vì A là giao điểm của BM và CN nên A nằm trên cả hai mặt phẳng (SBM) và (SCN). Ta có: S, A là hai điểm chung của hai mặt phẳng (SBM) và (SCN) nên giao tuyến của hai mặt phẳng này là đường SA.
|