Giải mục 2 trang 22, 23, 24 SGK Toán 11 tập 2 - Chân trời sáng tạo

Hoạt động 3

Cho \(s\) và \(t\) là hai đại lượng liên hệ với nhau theo công thức \(s = {2^t}\).

a) Với mỗi giá trị của \(t\) nhận giá trị trong \(\mathbb{R}\), tìm được bao nhiêu giá trị tương ứng của \(s\)? Tại sao?

b) Với mỗi giá trị của \(s\) thuộc \(\left( {0; + \infty } \right)\), có bao nhiêu giá trị tương ứng của \(t\)?

c) Viết công thức biểu thị \(t\) theo \(s\) và hoàn thành bảng sau.

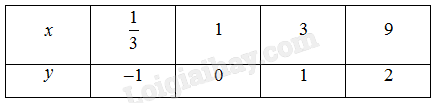
Phương pháp giải:

Sử dụng khái niệm hàm số, định nghĩa lôgarit.

Lời giải chi tiết:

a) Với mỗi giá trị của \(t\) thuộc \(\mathbb{R}\), tìm được duy nhất một giá trị tương ứng của \(s\).

b) Với mỗi giá trị của \(s\) thuộc \(\left( {0; + \infty } \right)\), có duy nhất một giá trị tương ứng của \(t\).

c) \(s = {2^t} \Leftrightarrow t = {\log _2}s\)

Ta có:

 

Hoạt động 4

a) Xét hàm số \(y = {\log _2}x\) với tập xác định \(D = \left( {0; + \infty } \right)\).

 

i) Hoàn thành bảng giá trị sau:

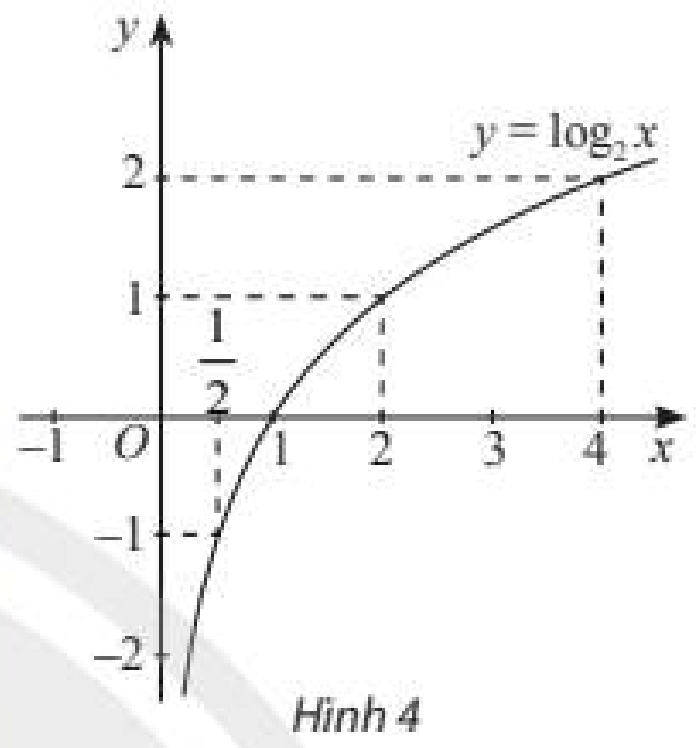
ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{{\log }_2}x} \right)\) với \(x > 0\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to  + \infty ,x \to {0^ + }\) và tập giá trị của hàm số đã cho.

b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\). Từ đó, nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to  + \infty ,x \to {0^ + }\) và tập giá trị của hàm số này.

Phương pháp giải:

a) Thay các giá trị của \(x\) vào hàm số sau đó dựa vào đồ thị nhận xét.

b) Lập bảng giá trị, vẽ đồ thị hàm số, sau đó dựa vào đồ thị nhận xét.

Lời giải chi tiết:

a) i)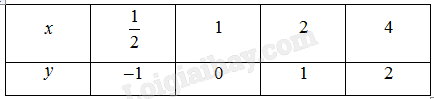

ii) ‒ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).

‒ Hàm số đồng biến trên \(\left( {0; + \infty } \right)\).

‒ Giới hạn: \(\mathop {\lim }\limits_{x \to  + \infty } {\log _2}x =  + \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x =  - \infty \).

‒ Tập giá trị: \(\mathbb{R}\).

b) Bảng giá trị:

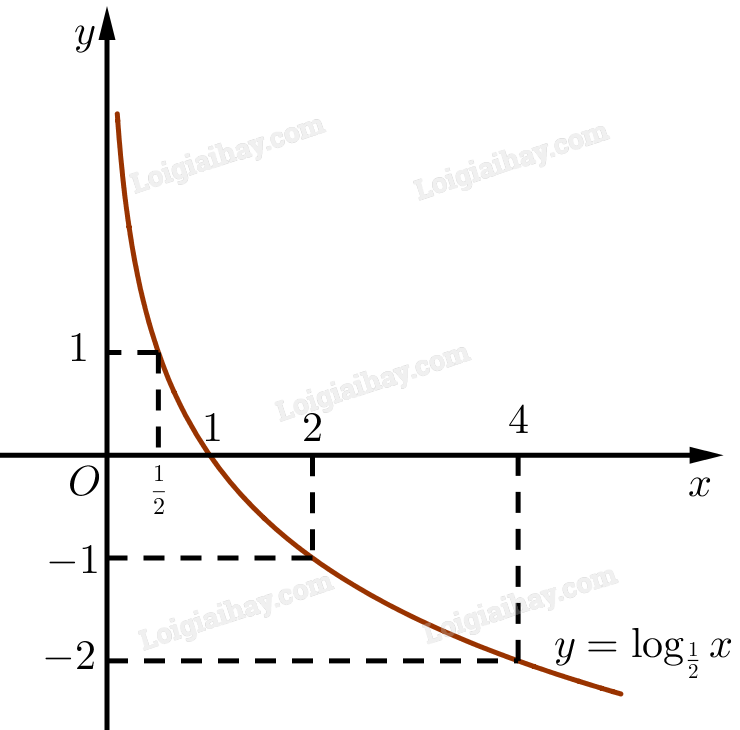
Đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\):

‒ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).

‒ Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).

‒ Giới hạn: \(\mathop {\lim }\limits_{x \to  + \infty } {\log _{\frac{1}{2}}}x =  - \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x =  + \infty \).

‒ Tập giá trị: \(\mathbb{R}\).

Thực hành 3

Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số \(y = {\log _3}x\) và \(y = {\log _{\frac{1}{3}}}x\).

Phương pháp giải:

Lập bảng giá trị, dựa vào bảng giá trị vẽ đồ thị.

Lời giải chi tiết:

Bảng giá trị:

‒ Hàm số \(y = {\log _3}x\):

‒ Hàm số \(y = {\log _{\frac{1}{3}}}x\):

‒ Đồ thị:

Thực hành 4

So sánh các cặp số sau:

a) \({\log _{\frac{1}{2}}}4,8\) và \({\log _{\frac{1}{2}}}5,2\);

b) \({\log _{\sqrt 5 }}2\) và \({\log _5}2\sqrt 2 \);

c) \( - {\log _{\frac{1}{4}}}2\) và \({\log _{\frac{1}{2}}}0,4\).

Phương pháp giải:

Sử dụng tính chất của hàm số lôgarit.

Lời giải chi tiết:

a) Hàm số \(y = {\log _{\frac{1}{2}}}x\) có cơ số \(\frac{1}{2} < 1\) nên nghịch biến trên \(\left( {0; + \infty } \right)\).

Mà \(4,8 < 5,2\) nên \({\log _{\frac{1}{2}}}4,8 > {\log _{\frac{1}{2}}}5,2\).

b) \({\log _{\sqrt 5 }}2 = {\log _{{5^{\frac{1}{2}}}}}2 = 2{\log _5}2 = {\log _5}{2^2} = {\log _5}4\)

Hàm số \(y = {\log _5}x\) có cơ số \(5 > 1\) nên đồng biến trên \(\left( {0; + \infty } \right)\).

Mà \(4 > 2\sqrt 2 \) nên \({\log _5}4 > {\log _5}2\sqrt 2 \). Vậy \({\log _{\sqrt 5 }}2 > {\log _5}2\sqrt 2 \)

c) \( - {\log _{\frac{1}{4}}}2 =  - {\log _{{{\left( {\frac{1}{2}} \right)}^2}}}2 =  - \frac{1}{2}{\log _{\frac{1}{2}}}2 = {\log _{\frac{1}{2}}}{2^{ - \frac{1}{2}}} = {\log _{\frac{1}{2}}}\frac{1}{{\sqrt 2 }}\)

Hàm số \(y = {\log _{\frac{1}{2}}}x\) có cơ số \(\frac{1}{2} < 1\) nên nghịch biến trên \(\left( {0; + \infty } \right)\).

Mà \(\frac{1}{{\sqrt 2 }} > 0,4\) nên \({\log _{\frac{1}{2}}}\frac{1}{{\sqrt 2 }} < {\log _{\frac{1}{2}}}0,4\). Vậy \( - {\log _{\frac{1}{4}}}2 < {\log _{\frac{1}{2}}}0,4\)

Vận dụng 2

Mức cường độ âm được tính theo công thức như ở Ví dụ 6.

a) Tiếng thì thầm có cường độ âm \(I = {10^{ - 10}}W/{m^2}\) thì có mức cường độ âm bằng bao nhiêu?

b) Để nghe trong thời gian dài mà không gây hại cho tai, âm thanh phải có cường độ không vượt quá 100 000 lần cường độ của tiếng thì thẩm. Âm thanh không gây hại cho tai khi nghe trong thời gian dài phải ở mức cường độ âm như thế nào?

Phương pháp giải:

Sử dụng công thức tính mức cường độ âm \(L = 10\log \left( {\frac{I}{{{I_0}}}} \right)\left( {dB} \right)\) với \({I_0} = {10^{ - 12}}W/{m^2}\).

Lời giải chi tiết:

a) Mức cường độ âm của tiếng thì thầm là:

\(L = 10\log \left( {\frac{I}{{{I_0}}}} \right) = 10\log \left( {\frac{{{{10}^{ - 10}}}}{{{{10}^{ - 12}}}}} \right) = 20\left( {dB} \right)\)

b) Để âm thanh không gây hại cho tai, âm thanh phải có cường độ âm không vượt quá:

\(I = {100000.10^{ - 10}} = 1{0^{ - 5}}W/{m^2}\)

Âm thanh không gây hại cho tai nghe trong thời gian dài phải ở mức cường độ âm không vượt quá:

\(L = 10\log \left( {\frac{I}{{{I_0}}}} \right) = 10\log \left( {\frac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}}} \right) = 70\left( {dB} \right)\)