Giải mục 1 trang 100, 101, 102 SGK Toán 11 tập 1 - Chân trời sáng tạo

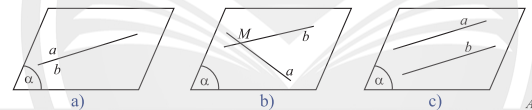
Hoạt động 1

a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng $a,b$ cùng nằm trong một mặt phẳng. 

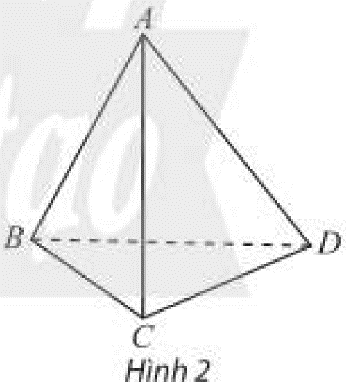
b) Cho tứ diện $ABCD$. Hai đường thẳng $AB$ và $CD$ có cùng nằm trong bất kì mặt phẳng nào không?

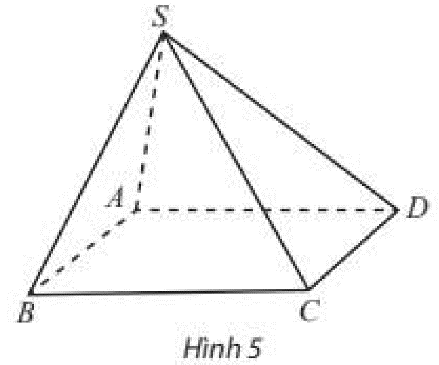
Phương pháp giải:

Quan sát hình ảnh, dựa vào vị trí tương đối của hai đường thẳng trong mặt phẳng.

Lời giải chi tiết:

a) Khi hai đường thẳng $a,b$ cùng nằm trong một mặt phẳng thì:

‒ Nếu $a,b$ có vô số điểm chung: Hai đường thẳng $a,b$ trùng nhau.

‒ Nếu $a,b$ có duy nhất một điểm chung: Hai đường thẳng $a,b$ cắt nhau.

‒ Nếu $a,b$ không có điểm chung: Hai đường thẳng $a,b$ song song với nhau.

b) Hai đường thẳng $AB$ và $CD$ không cùng nằm trong bất kì mặt phẳng nào.

Quảng cáo

Thực hành 1

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây:

a) $AB$ và $CD$;

b) $SA$ và $SC$;

c) $SA$ và $BC$.

Phương pháp giải:

Dựa vào vị trí tương đối của hai đường thẳng trong không gian:

• Trường hợp 1: Có một mặt phẳng chứa $a$ và $b$. Khi đó ta nói $a$ và $b$ đồng phẳng. Theo kết quả của hình học phẳng, có ba khả năng sau đây xảy ra:

‒ Nếu $a$ và $b$ có hai điểm chung thì ta nói $a$ trùng $b$.

‒ Nếu $a$ và $b$ có một điểm chung duy nhất M thì ta nói $a$ và $b$ cắt nhau tại M.

‒ Nếu $a$ và $b$ không có điểm chung thì ta nói $a$ và $b$ song song với nhau.

• Trường hợp 2: Không có mặt phẳng nào chứa cả $a$ và $b$. Khi đó ta nói hai đường thẳng $a$ và $b$ chéo nhau hay $a$ chéo với $b$.

Lời giải chi tiết:

a) $AB$ và $CD$ cùng nằm trong mặt phẳng $\left( {ABCD} \right)$.

$ABCD$ là hình bình hành nên $AB\parallel C{\rm{D}}$.

b) $SA$ và $SC$ cùng nằm trong mặt phẳng $\left( {SAC} \right)$.

Do đó $SA$ và $SC$ cắt nhau tại $S$.

c) Giả sử $SA$ và $BC$ cùng nằm trong mặt phẳng $\left( P \right)$.

Suy ra đường thẳng $AC$ cũng nằm trong $\left( P \right)$.

Do đó $\left( P \right)$ chứa cả 4 điểm của tứ diện $SABC$ (vô lí do $S$ không nằm trong mặt phẳng $\left( {ABCD} \right)$).

Vậy $SA$ và $BC$ không cùng nằm trong một mặt phẳng. Vậy $SA$ và $BC$ chéo nhau.

Vận dụng 1

Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

Phương pháp giải:

Quan sát, dựa vào vị trí tương đối của hai đường thẳng trong không gian.

Lời giải chi tiết:

‒ Hai thanh sắt đối diện nhau ở hai bên cầu song song với nhau.

‒ Hai thanh sắt liền nhau cùng nằm ở thành cầu hoặc mái cầu cắt nhau.

‒ Thanh sắt nằm ở mái cầu và thanh sắt nằm ở thành cầu chéo nhau.