Bài tập chủ đề 2 trang 39 Khoa học tự nhiên 9 Cánh diều

Bài 1

Trả lời câu hỏi bài 1 trang 39 SGK KHTN 9 Cánh diều

Chiếu tia sáng từ không khí vào rượu với góc tới bằng 60°. Biết chiết suất của rượu là 1,36. Tính góc khúc xạ trong trường hợp này.

Phương pháp giải:

Sử dụng biểu thức của định luật khúc xạ ánh sáng\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\), để xác định góc khúc xạ trong trường hợp này.

Lời giải chi tiết:

- Chiết suất của môi trường không khí là: \({n_1} \approx 1,0\)

- Chiết suất của môi trường rượu: \({n_2} = 1,36\)

- Định luật khúc xạ ánh sáng: \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}} =  > \sin r = \sin i.\frac{{{n_1}}}{{{n_2}}}\)

Thay số: \(\sin r = \sin 60.\frac{1}{{1,36}} \approx 0,637 =  > r = \arcsin (0,637) \approx {39^o}33'\)

Bài 2

Trả lời câu hỏi bài 2 trang 39 SGK KHTN 9 Cánh diều

Ở hình 3.3, nếu thay tia sáng đỏ bằng ánh sáng trắng thì có xảy ra hiện tượng tán sắc ánh sáng không? Vẽ hình giải thích dự đoán của em.

Phương pháp giải:

Sử dụng định nghĩa hiện tượng tán sắc ánh sáng (Khi chiếu chùm sáng trắng qua lăng kính, dùng màn chắn chùm tia ló thì trên màn quan sát thu được dải ánh sáng màu giống như dải màu cầu vồng (so với phương của tia tới, tia đỏ lệch ít nhất, tia tím lệch nhiều nhất), đó là quang phổ của ánh sáng trắng). Từ đó vận dụng vào ví dụ được nêu ở trên: ánh sáng mặt trời là ánh sáng trắng, lăng kính là khối thủy tinh. Từ đó, học sinh thiết kế thí nghiệm làm kiểm chứng giống với hình 3.3 trong sách giáo khoa.

Lời giải chi tiết:

Khi ánh sáng trắng chiếu vào khối thủy tinh, có thể xảy ra được hiện tượng tán sắc ánh sáng. Khi ánh sáng trắng chuyển từ không khí sang thủy tinh, ánh sáng bị phân tách và tạo ra dải màu sắc, giống như một cầu vồng.

Tuy nhiên, đối với thủy tinh, hiện tượng tán sắc này thường không rõ ràng bằng như với các vật liệu khác như viên pha lê hay các chất có cấu trúc tinh thể đặc biệt. Điều này là do cấu trúc của thủy tinh nên hiệu ứng tán sắc không được thể hiện rõ như trong một số vật liệu khác.

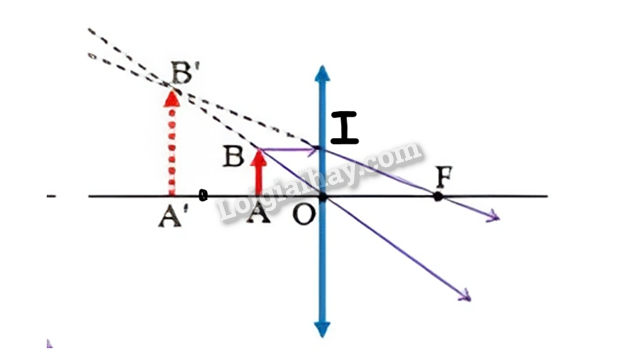
Bài 3

Trả lời câu hỏi bài 3 trang 39 SGK KHTN 9 Cánh diều

Ở hình 1, vì sao bông hoa hồng có màu đỏ và lá có màu xanh?

Hình 1

Phương pháp giải:

Sử dụng kiến thức có trong sách giáo khoa giải thích về ta thấy bông hồng màu đỏ, từ đó vận dụng tương tự với lá của chúng. (Màu sắc của các vật được tạo nên là do khi nhận được ánh sáng từ Mặt Trời, tùy theo vật liệu và tính chất ở bề mặt của các vật mà chúng sẽ hấp thụ một số ánh sáng màu và cho phản xạ một hoặc một số ánh sáng màu khác. Nếu ta thấy bông hoa hồng màu đỏ có nghĩa là những cánh hoa hồng đã hấp thụ các màu khác và cho phản xạ ánh sáng màu đỏ tới mắt.)

Lời giải chi tiết:

Dưới ánh nắng mặt trời, ta nhìn thấy bông hoa hông có màu đỏ vì cánh hoa hồng đã hấp thụ các màu khác và cho phản xạ ánh sáng màu đỏ tới mắt. Tương tự, ta nhìn thấy lá của bông hồng có màu xanh vì lá của hoa hồng đã hấp thụ các màu khác và cho phản xạ ánh sáng màu xanh tới mắt.

Bài 4

Trả lời câu hỏi bài 4 trang 39 SGK KHTN 9 Cánh diều

Dòng chữ trên trang sách được đặt cách thấu kính hội tụ 5 cm cho ảnh ảo có chiều cao gấp đôi. Tìm tiêu cự của thấu kính.

Phương pháp giải:

Bước 1. Tóm tắt để bài, ghi các kích thước đã cho.

Bước 2. Vẽ ảnh của vật qua thấu kính. (Các khoảng cách và chiều cao vật cần vẽ theo tỉ lệ thích hợp)

Bước 3. Dựa theo hai cặp tam giác đồng dạng thiết lập các tỉ số.

Bước 4. Giải các phương trình thu được.

Lời giải chi tiết:

Ta có: OA = 5 cm, A'B' = 2AB. Tìm OF.

Do ∆ОАВ ~ ∆OA'B' và ∆FA'B' ~ ∆FOI

Nên\(\frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}}\) \(\)(1)         \(\frac{{OF}}{{OA' + OF}} = \frac{{OI}}{{A'B'}}\)  (2)          OI=AB (3)

Từ (1), (2) và (3) ta có:

\(\begin{array}{l}\frac{{OF}}{{OA' + \;OF}} = \frac{{OI}}{{A'B'}} =  > \frac{{OF}}{{OA' + \;OF}} = \frac{{AB}}{{A'B'}} =  > \frac{{OF}}{{OA' + \;OF}} = \frac{{OA}}{{OA'}}\\ =  > OF.OA' = OA.OA' + OA.OF\\ =  > OF(OA' - OA) = OA.OA'\\ =  > \frac{1}{{\;OF}} = \frac{{OA' - OA}}{{OA'.OA}} =  > \frac{1}{{\;OA}} - \frac{1}{{\;OA'}} = \frac{1}{{OF}}\end{array}\)

Mà \(\frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}} = 2 =  > OA' = 2OA = 2.5 = 10cm\)

Thay số vào ta được: \(\frac{1}{{\;OA}} - \frac{1}{{\;OA'}} = \frac{1}{{OF}} =  > \frac{1}{{\;5}} - \frac{1}{{\;10}} = \frac{1}{{OF}} =  > OF = 10cm\)