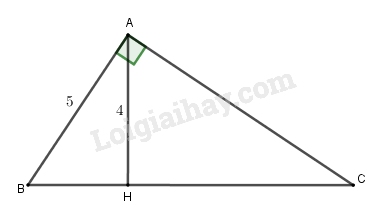
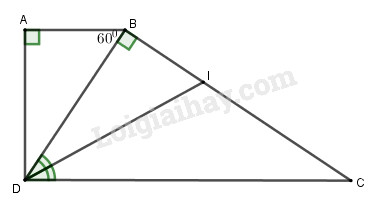
Đề kiểm tra 45 phút chương 3 phần Hình học 8 - Đề số 1

Đề bài

Câu 1:

Hãy chọn kết quả đúng. Tam giác $ABC$ vuông tại $A$ có độ dài $AB = 5cm$, đường cao $AH = 4cm$ (h.57).

a) Độ dài của $BH$ là:

A. $3,5$

B. $4$

C. $3$

D. $3,2$

b) Độ dài của $HC$ là:

A. $\dfrac{8}{3}$

B. $\dfrac{{20}}{3}$

C. $\dfrac{{16}}{3}$

D. $\dfrac{{15}}{4}$

c) Độ dài của $AC$ là:

A. $\dfrac{{20}}{3}$

B. $\dfrac{{25}}{3}$

C. $\dfrac{{25}}{{12}}$

D. $4\sqrt {\dfrac{5}{6}}$

Câu 2. (7 điểm) Cho hình thang vuông $ABCD$ $\left( {AB//CD} \right)$ có $\widehat A = {90^0}$, cạnh $BC$ vuông góc với đường chéo $BD$, đường phân giác của góc $BDC$ cắt cạnh $BC$ tại $I$. Cho biết độ dài $AB = 2,5cm$ và góc $\widehat {ABD} = {60^0}$ (h.58)

a) Chứng minh rằng $\Delta IDC$ là tam giác cân.

b) Tính độ dài của các cạnh $BC,AD,DC$ và độ dài của phân giác $DI$.

Lời giải chi tiết

Câu 1:

Phương pháp:

Sử dụng định lý Pi – ta – go trong tam giác vuông và tam giác đồng dạng để tính độ dài các cạnh.

Cách giải:

a) Tam giác $AHB$ vuông tại $H$ nên $B{H^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9$ $\Rightarrow BH = 3$.

Chọn C.

b) Xét tam giác $AHB$ và $CHA$ có:

$\widehat {AHB} = \widehat {CHA} = {90^0}\left( {gt} \right)$

$\widehat {HAB} = \widehat {HCA}$ (cùng phụ với góc $\widehat {CBA}$)

$\Rightarrow \Delta AHB \backsim \Delta CHA\left( {g.g} \right)$

$\Rightarrow \dfrac{{AH}}{{CH}} = \dfrac{{HB}}{{HA}}$ $\Rightarrow HC = \dfrac{{H{A^2}}}{{HB}} = \dfrac{{{4^2}}}{3} = \dfrac{{16}}{3}$

Chọn C.

c) Ta có: $BC = BH + HC = 3 + \dfrac{{16}}{3} = \dfrac{{25}}{3}$

Áp dụng định lí Pi – ta – go cho tam giác vuông $ABC$ có:

$A{C^2} = B{C^2} - A{B^2}$ $= {\left( {\dfrac{{25}}{3}} \right)^2} - {5^2} = \dfrac{{400}}{9}$ $\Rightarrow AC = \dfrac{{20}}{3}$

Chọn A.

Câu 2:

Phương pháp:

a) Chứng minh tam giác $IDC$ có hai góc $\widehat {IDC} = \widehat {ICD}$ và suy ra $IC = ID$.

b) Sử dụng các tam giác đồng dạng và định lí Pi – ta – go để tính toán.

Chú ý kết quả: Tam giác vuông có một góc bằng ${30^0}$ thì cạnh đối cửa góc bằng nửa cạnh huyền.

Cách giải:

a) Tam giác $ABC$ vuông tại $A$ có:

$\widehat {ABD} + \widehat {ADB} = {90^0}$ (hai góc nhọn trong tam giác vuông)

$\Rightarrow \widehat {ADB} = {90^0} - \widehat {ABD}$ $= {90^0} - {60^0} = {30^0}$

$\Rightarrow \widehat {BDC} = \widehat {ADC} - \widehat {ADB}$ $= {90^0} - {30^0} = {60^0}$

$\Rightarrow \widehat {IDB} = \widehat {IDC} = \dfrac{{\widehat {BDC}}}{2}$ $= \dfrac{{{{60}^0}}}{2} = {30^0}$ (1)

Tam giác $BDC$ vuông tại $B$ có $\widehat {BDC} + \widehat {BCD} = {90^0}$ (hai góc nhọn trong tam giác vuông)

$\Rightarrow \widehat {BCD} = {90^0} - \widehat {BDC}$ $= {90^0} - {60^0} = {30^0}$ hay $\widehat {ICD} = {30^0}$ (2)

Từ (1) và (2) suy ra $\widehat {IDC} = \widehat {ICD}$ nên tam giác $ICD$ cân tại $I$

$\Rightarrow ID = IC$ (đpcm).

b) Tam giác $ABC$ vuông tại $A$ có $\widehat {ADB} = {30^0}$ nên $AB = \dfrac{1}{2}BD$

$\Rightarrow BD = 2AB = 2.2,5 = 5\left( {cm} \right)$

Áp dụng định lí Pi – ta – go ta có:

$A{D^2} = B{D^2} - A{B^2}$ $= {5^2} - 2,{5^2} = \dfrac{{75}}{4}$ $\Rightarrow AD = \sqrt {\dfrac{{75}}{4}}  \approx 4,33\left( {cm} \right)$

Tam giác $BDC$ vuông tại $B$ có $\widehat {BCD} = {30^0}$ nên $BD = \dfrac{1}{2}DC$

$\Rightarrow DC = 2BD = 2.5 = 10\left( {cm} \right)$

Áp dụng định lí Pi – ta – go ta có:

$B{C^2} = C{D^2} - B{D^2} = {10^2} - {5^2} = 75$ $\Rightarrow BC = \sqrt {75}  \approx 8,66$.

Ta có: $\dfrac{{IB}}{{IC}} = \dfrac{{DB}}{{DC}} = \dfrac{1}{2}$ $\Rightarrow IC = 2IB$

Mà $IC + IB = BC = 8,66$ $\Rightarrow 2IB + IB = 8,66$ $\Rightarrow 3IB = 8,66 \Rightarrow IB \approx 2,89$

Áp dụng định lí Pi – ta – go ta có:

$D{I^2} = D{B^2} + B{I^2} = {5^2} + 2,{89^2}$ $\Rightarrow DI = \sqrt {{5^2} + 2,{{89}^2}}  \approx 5,78\left( {cm} \right)$.

HocTot.Nam.Name.Vn