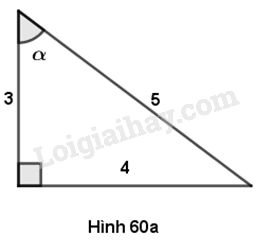
Đề kiểm tra 45 phút chương 1 phần Hình học 9 - Đề số 2

Đề bài

Câu 1 (3 điểm). Hãy chọn kết quả đúng

1. Trong hình 60a, $\sin \alpha$ bằng 

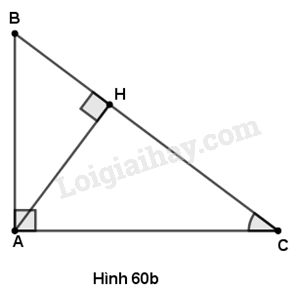
(A) $\dfrac{5}{4}$                            (B) $\dfrac{5}{3}$

(C) $\dfrac{4}{5}$                            (D) $\dfrac{3}{5}$

2. Trong hình 60b, cos C bằng:

(A) $\dfrac{{AB}}{{AC}}$                                    (B) $\dfrac{{AH}}{{AC}}$

(C) $\dfrac{{AB}}{{BC}}$                                     (D) $\dfrac{{CH}}{{AC}}$

3. Cho hai góc nhọn $\alpha$ và $\beta$ phụ nhau. Khi đó ta có:

(A) ${\sin ^2}\alpha  + {\cos ^2}\beta  = 1$

(B) $\sin \alpha  = \cos \beta$

(C) $\tan \alpha  = \cot \left( {{{90}^o} - \beta } \right)$

(D) $\sin \alpha  = \cos \left( {{{90}^o} - \beta } \right)$

Câu 2 (3 điểm). Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn $NA = 3$ và $PQ  = 6.$ Hãy so sánh cot N và cot P. Tỉ số nào lớn hơn và lớn hơn mấy lần ?

Câu 3 (4 điểm). Một em học sinh đứng ở mặt đất cách tháp ăng – ten 150m. Biết rằng em nhìn thấy đỉnh tháp ở góc 20^o so với đường nằm ngang và khoảng cách từ mắt em đến mặt đất là 1m. Hãy tính chiều cao của tháp.

Lời giải chi tiết

Câu 1:

Phương pháp giải :

1. Áp dụng $\sin \alpha  = \dfrac{{cạnh\,{\rm{ }}đối}}{{cạnh\,{\rm{ }}huyền}}$

2. Áp dụng $\cos C = \dfrac{{cạnh\,{\rm{ }}kề}}{{cạnh{\rm{ }}\,huyền}}$

3. Vận dụng kiến thức : Hai góc $\alpha$ và $\beta$ phụ nhau $\left( {\alpha  + \beta  = {{90}^o}} \right)$. Ta có:$\sin \alpha  = \cos \beta ;\,\,\cos \alpha  = \sin \beta ;$ $\,\tan \alpha  = \cot \beta ;\,\,\cot \alpha  = \tan \beta$.

Lời giải : 

1. $\sin \alpha  = \dfrac{{cạnh{\rm{ }}\,đối}}{{cạnh{\rm{ }}\,huyền}} = \dfrac{4}{5}$

Chọn C.

2. $\cos C = \dfrac{{cạnh\,{\rm{ }}kề}}{{cạnh{\rm{ }}\,huyền}} = \dfrac{{AC}}{{BC}} = \dfrac{{HC}}{{AC}}$

Chọn D.

3. Hai góc nhọn $\alpha$ và $\beta$ phụ nhau thì $\sin \alpha  = \cos \beta$

Chọn B.

Câu 2:

Phương pháp giải :

- Áp dụng tỉ số lượng giác $\cot \alpha  = \dfrac{{cạnh\,{\rm{ }}kề}}{{cạnh\,{\rm{ }}đối}}$ tìm $\cot N$ và $\cot P.$

- So sánh và tìm tỉ số $\dfrac{{\cot N}}{{\cot P}}$ để trả lời câu hỏi tỉ số lớn hơn mấy lần.

Lời giải :

Tam giác vuông $MNQ$ có :$\cot N = \dfrac{{NQ}}{{MQ}} = \dfrac{3}{{MQ}}$

Tam giác vuông $MPQ$ có : $\cot P = \dfrac{{QP}}{{MQ}} = \dfrac{6}{{MQ}}$

Vì $MQ$ là đường cao của $\Delta MNP$ nên độ dài $MQ$ cố định và $MQ \ne 0.$

Mà $\dfrac{3}{{MQ}} < \dfrac{6}{{MQ}} \Rightarrow \cot N < \cot P.$

Xét tỉ số $\cot N:\cot P = \dfrac{3}{{MQ}}:\dfrac{6}{{MQ}} = \dfrac{3}{6} = \dfrac{1}{2}$ $\Rightarrow \cot P = 2.\cot N$

Vậy $\cot P$ lớn hơn $\cot N$ và lớn hơn gấp $2$ lần.

Câu 3:

Phương pháp giải :

- Vẽ hình biểu diễn các thông tin của bài toán.

- Chiều cao của tháp ăng-ten bằng tổng độ dài của $BC$ và $AB.$  

- Tìm độ dài $BC$ dựa vào kiến thức : Trong tam giác vuông, cạnh góc vuông này bằng cạnh góc vuông kia nhân tang góc đối.

Lời giải :

Giả sử khoảng cách từ em học sinh đến tháp ăng-ten là đoạn $AE;$ mắt em là điểm $D$ thì chiều cao của tháp là đoạn $AC.$

Ta có $DB = AE$ (đều là khoảng cách từ em học sinh đến tháp ăng-ten)

Tam giác vuông $ABD$ có : $BC = BD.\tan \widehat {CDB}$$= 150.\tan {20^o} \approx 54,6m.$

Vậy chiều cao của tháp là : $AC = BC + CA$$= 54,6 + 1 = 55,6(m).$

HocTot.Nam.Name.Vn