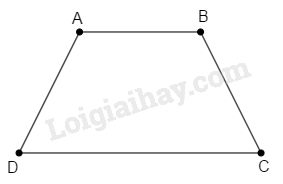
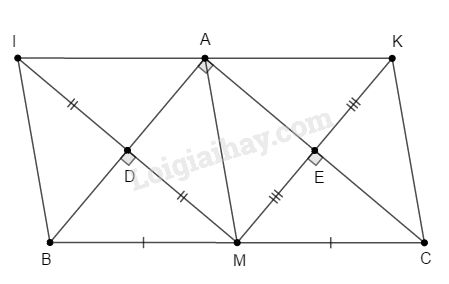
Đề kiểm tra 45 phút chương 1 phần Hình học 8 - Đề số 1

Đề bài

Câu 1: Cho hình thang $ABCD (AB//CD).$ Các khẳng định sau đúng hay sai?

a) Nếu $\widehat{A}+\widehat{D}={{180}^{o}}$  thì $ABCD$ là hình thang cân.

b) Nếu $\widehat{B}+\widehat{D}={{180}^{o}}$  thì $ABCD$ là hình thang cân.

Câu 2: Hình vuông có đường chéo bằng $\sqrt {18}$  thì cạnh bằng

(A) $2$                           (B) $3$

(C) $6$                           (D) $\sqrt 3$

Hãy chọn câu trả lời đúng.

Câu 3: Xét các tam giác vuông $ABC$ có cạnh huyền $BC$ cố định, $BC = 4 cm$, $I$ là trung điểm của $BC$. Tập hợp các điểm $A$ là

(A) Đường tròn $(B;2cm)$

(B) Đường tròn $(C;2cm)$

(C) Đường tròn $(I;2cm)$

(D) Đường tròn $(I;4cm)$

Hãy chọn câu trả lời đúng.

Câu 4: Cho tam giác $ABC$ vuông tại $A, M$ là trung điểm của $BC.$ Gọi $I$ là điểm đối xứng với $M$ qua $AB,$ gọi $D$ là giao điểm của $MI$ và $AB.$ Gọi $K$ là điểm đối xứng với $M$ qua $AC,$ gọi $E$ là giao điểm của $MK$ và $AC.$

a) Tứ giác $ADME$ là hình gì? Vì sao?

b) Tứ giác $AMCK$ là hình gì? Vì sao?

c) Chứng minh hai điểm $I$ và $K$ đối xứng với nhau qua điểm $A.$

d) Nếu tam giác $ABC$ vuông cân tại $A$ thì các tứ giác $ADME, AMCK$ là hình gì? Vì sao? Vẽ hình tương ứng.

Lời giải chi tiết

Câu 1:

Phương pháp:

Sử dụng: 

- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.

- Hình thang có hai góc kề với một đáy bằng nhau là hình thang cân.

Lời giải:

Vì $AB//CD$ nên $\widehat{A}+\widehat{D}={{180}^{o}}$  (1)  (hai góc trong cùng phía).

$\widehat{B}+\widehat{D}={{180}^{o}}$             (2)

Từ (1) và (2) suy ra $\widehat{A}=\widehat{B}$ nên ABCD là hình thang cân.

Do đó a) sai; b) đúng.

Câu 2: 

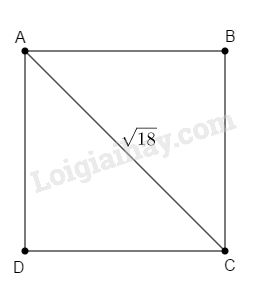
Phương pháp:

Sử dụng: 

- Hình vuông là tứ giác có bốn cạnh bằng nhau, bốn góc bằng nhau.

- Định lí Pytago: Bình phương của cạnh huyền bằng bình phương của hai cạnh góc vuông.

Lời giải:

Gọi cạnh hình vuông là $a$ $(a>0)$.

Áp dụng định lí Pytago vào $\Delta ADC$  vuông tại $D$ ta có:

$\begin{align}& A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}} \\& {{a}^{2}}+{{a}^{2}}={{\left( \sqrt{18} \right)}^{2}} \\& 2{{a}^{2}}=18 \\& \Rightarrow {{a}^{2}}=18:2=9 \\ & \Rightarrow a=\sqrt{9}=3 \\\end{align}$

Chọn B.

Câu 3: 

Phương pháp:

Sử dụng: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.

Lời giải:

$AI$ là đường trung tuyến ứng với cạnh huyền $BC$ nên $AI=BC:2=4:2=2cm$

$I$ là trung điểm của $BC$, mà $BC$ cố định nên $I$ cố định. Do đó tập hợp các điểm $A$ là đường tròn $(I;2cm)$.

Chọn C.

 Câu 4:

Phương pháp:

- Tứ giác có ba góc vuông là hình chữ nhật. 

- Tứ giác có hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường là hình thoi.

- Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.

Lời giải: 

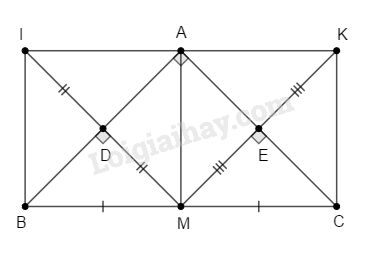
a) $I$ đối xứng $M$ qua $AB$ nên $AB$ là trung trực của $MI.$ Do đó $\widehat {ADM} = {90^o}$

$K$ đối xứng $M$ qua $AC$ nên $AC$ là trung trực của $MK.$ Do đó $\widehat {AEM} = {90^o}$

Tứ giác $ADME$ có $\widehat {ADM} = \widehat {AEM} = \widehat {DAE} = {90^o}$  nên là hình chữ nhật( Tứ giác có 3 góc vuông).

b) $AM$ là trung tuyến ứng với cạnh huyền $BC$ của $\Delta ABC$  nên $AM=MC$

Xét hai tam giác vuông $AME$ và $CME$ có:

$AM=MC$ (chứng minh trên)

$ME$ chung

$\widehat{AEM}=\widehat{CEM}={{90}^{o}}$

$\Rightarrow \Delta AME = \Delta CME$  (cạnh huyền – cạnh góc vuông).

$\Rightarrow AE=CE$  (hai cạnh tương ứng).

Tứ giác $AMCK$ có hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường nên là hình thoi.

c) $AMCK$ là hình thoi nên $AK=MC; AK//BC$    (1)

Chứng minh tương tự ta được: $AMBI$ là hình thoi

Suy ra $AI=BM; AI//BM$     (2)

Từ (1) và (2) suy ra $AK=AI.$

Qua $A$ có hai đường thẳng cùng song song với $BC$ nên theo tiên đề Ơclit $I, A,K$ thẳng hàng.

Do đó $I$ và $K$ đối xứng với nhau qua điểm $A.$

d) Tam giác $ABC$ vuông cân tại $A$ thì $AD=AE$ nên $ADME$ là hình vuông( Hình chữ nhật có 2 cạnh kề bằng nhau);

$AE = ME \Rightarrow AC = MK$  do đó $AMCK$ là hình vuông ( Hình thoi có 2 đường chéo bằng nhau).

Hình vẽ tương ứng:

HocTot.Nam.Name.Vn