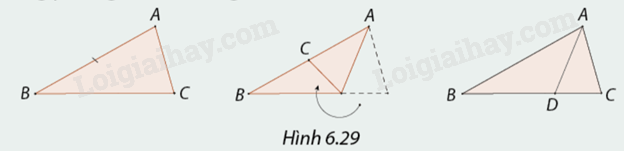
Giải câu hỏi trang 46, 47 SGK Toán 8 - Cùng khám phá1. Cắt tam giác \(ABC\) bất kì có \(AB = 2AC.\) Gấp giấy sao cho cạnh \(AC\) chồng lên
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 1. Cắt tam giác \(ABC\) bất kì có \(AB = 2AC.\) Gấp giấy sao cho cạnh \(AC\) chồng lên cạnh \(AB\) để xác định đường phân giác \(AD\) (Hình 6.29). Đo độ dài các đoạn thẳng \(BD,CD.\) Tính và so sánh tỉ số \(\frac{{BD}}{{CD}}\) và \(\frac{{AB}}{{AC}}.\) 2. Thực hiện tương tự với trường hợp \(\frac{{AB}}{{AC}} = \frac{3}{2}.\) Em có nhận xét gì về vị trí chân đường phân giác của tam giác?
Phương pháp giải: Đo độ dài các đoạn thẳng \(BD,CD.\) Sau đó tính và so sánh tỉ số \(\frac{{BD}}{{CD}}\) và \(\frac{{AB}}{{AC}}\) dựa vào tỉ lệ của hai đoạn thẳng. Lời giải chi tiết: 1. Gọi số đo AC là 1 thì số đo AB là 2. Đo độ dài đoạn thẳng \(BD = 2;CD = 1\) Tỉ số \(\frac{{BD}}{{CD}} = \frac{2}{1} = 2\) Tỉ số \(\frac{{AB}}{{AC}} = \frac{2}{1} = 2\) Ta thấy \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = 2\) . 2. Với \(AB = 3;AC = 2\) thì số đo độ dài đoạn thẳng \(BD = 3;CD = 2\) Ta thấy tỉ số \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{3}{2}\) Từ hai trường hợp trên, ta thấy dựa vào độ dài cạnh ta xác định được vị trí chân đường phân giác của một tam giác. Luyện tập Tìm độ dài cạnh \(AC\) trong Hình 6.32.
Phương pháp giải: Dựa vào tính chất đường phân giác của một tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy. Lời giải chi tiết: Xét tam giác \(ABC\) , ta có: \(\widehat {BAD} = \widehat {DAC}\) (gt) => AD là đường phân giác Áp dụng tính chất đường phân giác ta có: \(\frac{{BA}}{{AC}} = \frac{{BD}}{{DC}} \Leftrightarrow \frac{{10}}{{AC}} = \frac{{7,5}}{{10,5}} \Rightarrow AC = 14\) Vận dụng Bác thợ mộc cần cưa mảnh ván hình tam giác \(ABC\) thành hai phần theo đường phân giác \(BD\) của góc \(B\) (Hình 6.33), nhưng bác chỉ có thước đo độ dài. Bác đo được \(AB = 60\,cm,AC = 100cm\) và \(BC = 140cm.\) Hãy giúp bác xác định vị trí điểm \(D\) và vẽ đường cưa.
Phương pháp giải: Dựa vào tính chất đường phân giác của một tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy. Lời giải chi tiết: Áp dụng tính chất đường phân giác ta có: \(\frac{{AD}}{{DC}} = \frac{{BA}}{{BC}} \Leftrightarrow \frac{x}{{100 - x}} = \frac{{60}}{{140}} \Leftrightarrow \frac{x}{{100 - x}} = \frac{3}{7} \Leftrightarrow 7x = 300 - 3x \Rightarrow x = 30\) Vậy \(AD = 30;DC = 100 - 30 = 70\)
|