Giải câu hỏi trang 4 SGK Toán 8 - Cùng khám pháBàn cờ vua có 8 cột
Lựa chọn câu để xem lời giải nhanh hơn
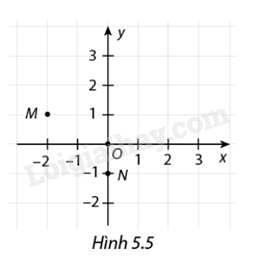
Hoạt động Bàn cờ vua có 8 cột (a,b,c,d,e,f,g,h) và 8 hàng (1,2,3,4,5,6,7,8). Trong Hình 5.1, trên bàn cờ của ván đang chơi còn một quân mã. a) Xác định vị trí của quân mã trên bàn cờ. Giải thích cách xác định vị trí đó. b) Xác định các vị trí quân mã này có thể di chuyển đến sau một nước đi từ ô đang đứng, biết rằng theo quy tắc chơi, quân mã được di theo đường chéo của hình chữ nhật có kích thước 2×3 ô. Phương pháp giải: Ta dùng hai yếu tố hàng ngang và cột dọc để xác định vị trí của quân mã và xác định các vị trí quân mã này có thể di chuyển đến sau một nước đi từ ô đang đứng. Lời giải chi tiết: a) Vị trí của quân mã trên bàn cờ: hàng số 8 cột b b) Các vị trí quân mã có thể di chuyển đến sau một nước đi từ ô đang đứng: Hàng 6 cột a Hàng 6 cột c Hàng 7 cột d Luyện tập 1 Cho Hình 5.5. a) Xác định tọa độ các điểm O,M,N. b) Xác định tọa độ điểm P tùy ý thuộc Ox, tọa độ điểm Q tùy ý thuộc Oy.
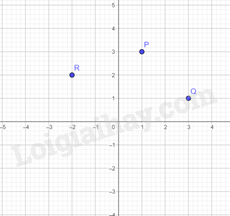
Phương pháp giải: Trong mặt phẳng tọa độ Oxy, mỗi điểm M được xác định bởi cặp số (x0;y0) và ngược lại Cặp số (x0;y0) được gọi là tọa độ của điểm M. Số x0 gọi là hoành độ và số y0 gọi là tung độ của điểm M. Nếu (x0;y0) là tọa độ của điểm M thì ta viết là M(x0;y0). Lời giải chi tiết: a) Quan sát Hình 5.5. Xét điểm O ta thấy các đường thẳng vuông góc kẻ từ điểm O xuống trục hoành và trục tung bằng chính điểm O vậy ta có tọa độ O(0;0). Tương tự với điểm M có tọa độ là M(−2;1) và điểm N có tọa độ là N(0;−1). b) Tọa độ điểm P tùy ý thuộc Ox thì sẽ có hoành độ bằng 0: P(2;0) Tọa độ điểm Q tùy ý thuộc Oy thì sẽ có tung độ bằng 0: Q(−2;0) Luyện tập 2 Vẽ một hệ trục tọa độ Oxy và đánh dấu vị trí của các điểm P(1;3),Q(3;1),R(−2;2) Mỗi điểm này thuộc góc phần tư nào của mặt phẳng tọa độ? Phương pháp giải: Dựa vào cách vẽ mặt phẳng tọa độ và cách xác định vị trí tọa độ các điểm để vẽ được hệ trục tọa độ Oxy và đánh dấu vị trí của các điểm. Lời giải chi tiết:
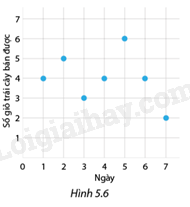
Điểm P thuộc góc phần tư thứ I của mặt phẳng tọa độ Điểm Q thuộc góc phần tư thứ I của mặt phẳng tọa độ Điểm R thuộc góc phần tư thứ II của mặt phẳng tọa độ Vận dụng Hình 5.6 biểu diễn số giỏ trái cây bán được trong tuần đầu khai trương của một cửa hàng. a) Trong ngày đầu khai trường, cửa hàng bán được bao nhiêu giỏ trái cây? b) Cửa hàng bán được nhiều giỏ trái cây nhất vào ngày thứ mấy trong tuần đầu khai trương và bán được bao nhiêu giỏ?
Phương pháp giải: Dựa vào cách xác định vị trí tọa độ điểm trong mặt phẳng tọa độ để xác định cửa hàng bán được bao nhiêu giỏ trái cây trong ngày đầu khai trương và bán được nhiều nhất vào ngày thứ mấy. Lời giải chi tiết: a) Trong ngày đầu khai trương, cửa hàng bán được 4 giỏ trái cây b) Cửa hàng bán được nhiều giỏ trái cây nhất vào ngày thứ 5 bán được 6 giỏ trái cây.
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|