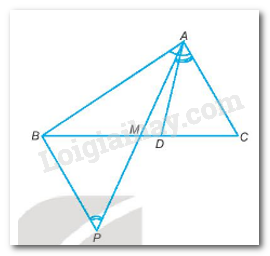
Giải Bài 9.4 trang 48 sách bài tập toán 7 - Kết nối tri thức với cuộc sốngCho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC. a)Hãy so sánh hai góc MAB và MAC. b)Tia phân giác của góc BAC cắt BC tại D. Hỏi D thuộc đoạn thẳng MB hay đoạn thẳng MC? Vì sao? Đề bài Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC. a)Hãy so sánh hai góc MAB và MAC. b)Tia phân giác của góc BAC cắt BC tại D. Hỏi D thuộc đoạn thẳng MB hay đoạn thẳng MC? Vì sao? Phương pháp giải - Xem chi tiết a) - Lấy điểm P sao cho M là trung điểm của AP. -Chứng minh: \(\Delta AMC = \Delta PMB\left( {c - g - c} \right)\) -Chứng minh: \(\widehat {MPB} > \widehat {MAB}\) Lời giải chi tiết
a) Lấy điểm P sao cho M là trung điểm của AP. Xét \(\Delta AMC\) và \(\Delta PMB\)có: AM = PM MC = MB \(\widehat {AMC} = \widehat {PMB}\) \( \Rightarrow \Delta AMC = \Delta PMB\left( {c - g - c} \right)\) Do AB > AC suy ra AB > PB Xét tam giác ABP có AB > PB \(\begin{array}{l} \Rightarrow \widehat {MPB} > \widehat {MAB}\\ \Rightarrow \widehat {MAC} > \widehat {MAB}\end{array}\) b) Ta có: AD là tia phân giác của góc BAC nên \(\widehat {DAB} = \widehat {DAC} = \dfrac{{\widehat {BAC}}}{2} \Rightarrow \widehat {BAC} = 2\widehat {DAC}\) Lại có: \(\begin{array}{l}\widehat {MAC} > \widehat {MAB}\left( {cmt} \right)\\ \Rightarrow \widehat {MAC} + \widehat {MAC} > \widehat {MAB} + \widehat {MAC}\\ \Rightarrow 2\widehat {MAC} > \widehat {BAC}\\ \Rightarrow 2\widehat {MAC} > 2\widehat {DAC}\\ \Rightarrow \widehat {MAC} > \widehat {DAC}\end{array}\) Vậy D thuộc đoạn thẳng MC.
|