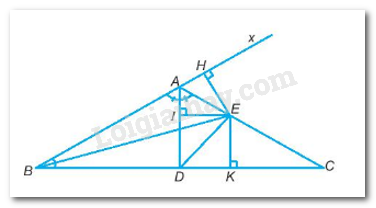
Giải Bài 9.17 trang 55 sách bài tập toán 7 - Kết nối tri thức với cuộc sốngTam giác ABC có AD, BE là hai đường phân giác và Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Tam giác ABC có AD, BE là hai đường phân giác và \(\widehat {BAC} = {120^0}\). Chứng minh rằng DE là tia phân giác của góc ADC. Phương pháp giải - Xem chi tiết - Gọi Ax là tia đối của tia AB -Chứng minh: \(\widehat {BAD} = \widehat {DAC} = \widehat {CAx}\) - Hạ \(EH \bot Bx;EI \bot AD;EK \bot BC\) -Áp dụng điểm nằm trên tia phân giác của góc thì cách đều 2 cạnh của của góc đó. Lời giải chi tiết
Gọi Ax là tia đối của tia AB \(\widehat {CAx} = {180^0} - \widehat {BAC} = {180^0} - {120^0} = {60^0}\) (2 góc kề bù) AD là phân giác góc BAC \( \Rightarrow \widehat {BAD} = \widehat {DAC} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\) \( \Rightarrow \widehat {BAD} = \widehat {DAC} = \widehat {CAx}\) Hạ \(EH \bot Bx;EI \bot AD;EK \bot BC\) Ta có: EH = EK (vì BE là phân giác góc ABC) EH = EI (vì AE là phân giác góc DAx) \( \Rightarrow EK = EI\) Vậy E nằm trên tia phân giác của góc ADC.
|