Bài 89 trang 121 SBT toán 9 tập 1

Đề bài

Cho hình thang với đáy nhỏ là \(15cm\), hai cạnh bên bằng nhau và bằng \(25cm\), góc tù bằng \(120^\circ \). Tính chu vi và diện tích của hình thang đó.

Lời giải chi tiết

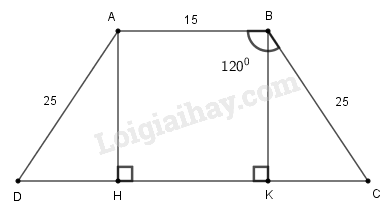
Giả sử hình thang \(ABCD\) có đáy nhỏ \(AB = 15cm\), cạnh bên \(AD = BC \)\(=25cm\), \(\widehat {ABC} = \widehat {BAD} = 120^\circ \).

Kẻ \(AH \bot CD,BK \bot CD\)

Ta có: \(AB//HK\) và \(AH//BK\) (cùng vuông với CD) nên \(ABKH\) là hình bình hành.

Suy ra: \(HK=AB  =15 (cm)\) và \(AH=BK\) 

Vì AB//CD nên \(\widehat {ADC} + \widehat {DAB} = 180^\circ \) (hai góc trong cùng phía)

Suy ra:

\(\widehat {ADC} = 180^\circ  - \widehat {DAB} = 180^\circ  - 120^\circ\)\(  = 60^\circ \)

Trong tam giác vuông \(ADH\), ta có:

\(\eqalign{
& DH = AD.\cos \widehat {ADC} \cr 
& = 25.\cos 60^\circ = 12,5\,(cm) \cr} \)

\(\eqalign{
& AH = AD.\sin \widehat {ADC} \cr 
& = 25.\sin 60^\circ = {{25\sqrt 3 } \over 2}(cm) \cr} \)

Ta có: \(AH=BK\) (cmt) và \(AD=BC\) (gt) nên hai tam giác vuông \(∆ADH=∆BCK\) (cạnh huyền - cạnh góc vuông)

Suy ra: \( CK =DH= 12,5 (cm)\)

Ta có: \(CD=CK + KH + HD\)\(=12,5 + 15 + 12,5=40cm\)

Chu vi hình thang \(ABCD\) là:

\(AB + BC + CD + DA \)

\(= 15 + 25 + 40 + 25\)

\( = 105 (cm)\)

Diện tích hình thang \(ABCD\) là:

\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr 
& = {{15 + 40} \over 2}.{{25\sqrt 3 } \over 2} \approx 595,392\,\,\left( {c{m^2}} \right) \cr} \)

HocTot.Nam.Name.Vn