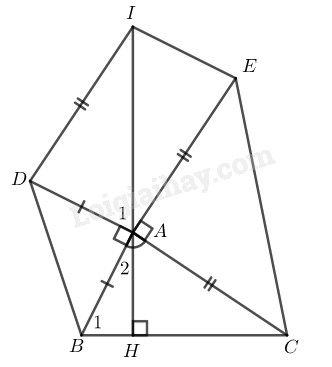
Bài 88 trang 90 SBT toán 8 tập 1

Đề bài

Cho tam giác \(ABC.\) Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại \(A\) là \(ABD, ACE.\) Vẽ hình bình hành \(ADIE.\) Chứng minh rằng:

\(a)\) \(IA = BC.\)

\(b)\) \(IA ⊥ BC.\)

Lời giải chi tiết

\(a)\) \(\widehat {BAC} + \widehat {BAD} + \widehat {DAE} + \widehat {EAC} = {360^0}\)

    \(\widehat {BAD} = {90^0},\widehat {EAC} = {90^0}(gt)\)

Suy ra: \(\widehat {BAC} + \widehat {DAE} = {180^0}\) \((1)\)

Lại có \( AE // DI\;\; \) (do ADIE là hình bình hành)

\(⇒\) \(\widehat {ADI} + \widehat {DAE} = {180^0}\) (hai góc trong cùng phía) \((2)\)

Từ \((1)\) và \((2)\) suy ra:  \(\widehat {BAC} = \widehat {ADI}\)

Xét \(∆ ABC\) và \(∆ DAI :\)

\(AB = AD \;\;(gt)\)

\(\widehat {BAC} = \widehat {ADI}\) (chứng minh trên)

\(AC = DI\) (vì cùng bằng \(AE\))

Do đó: \(∆ ABC = ∆ DAI \;\;(c.g.c)\)

\(⇒ IA = BC\)

\(b)\) \(∆ ABC = ∆ DAI\) ( chứng minh trên)

\( \Rightarrow {\widehat A_1} = {\widehat B_1}\)  \((3)\)

Gọi giao điểm \(IA\) và \(BC\) là \(H.\)

Ta có: \({\widehat A_1} + \widehat {BAD} + {\widehat A_2} = {180^0}\) (do H, A, I thẳng hàng)

mà \(\widehat {BAD} = {90^0}(gt)\)

\( \Rightarrow {\widehat A_1} + {\widehat A_2} = {90^0}\) \((4)\)

Từ \((3)\) và \((4)\) suy ra: \({\widehat B_1} + {\widehat A_2} = {90^0}\)

Trong \(∆ AHB\) ta có: \(\widehat {AHB} + \widehat {{B_1}} + {\widehat A_2} = {180^0}\)

Suy ra \(\widehat {AHB} = {90^0} \Rightarrow AH \bot BC\) hay \(IA ⊥ BC\)

HocTot.Nam.Name.Vn