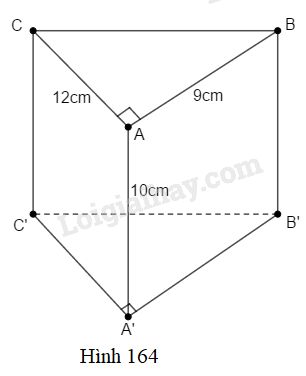
Bài 84 trang 156 SBT toán 8 tập 2Giải bài 84 trang 156 sách bài tập toán 8. Tìm diện tích toàn phần và thể tích của lăng trụ đứng có các kích thước như ở hình 164. Đề bài Tìm diện tích toàn phần và thể tích của lăng trụ đứng có các kích thước như ở hình \(164.\)
Phương pháp giải - Xem chi tiết Sử dụng: - Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao. \({S_{xq}} = 2p.h\) Trong đó: \(p\) là nửa chu vi đáy, \(h\) là chiều cao. - Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy. - Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao. \(V = S. h\) Trong đó: \(S\) là diện tích đáy; \(h\) là chiều cao lăng trụ. Lời giải chi tiết Áp dụng định lí Py-ta-go vào tam giác vuông \(ABC\), ta có: \(B{C^2} = A{B^2} + A{C^2} = {9^2} + {12^2} = 225\) \( \Rightarrow BC = 15\; (cm)\) Diện tích xung quanh hình lăng trụ là: \({S_{xq}} =(AB+AC+BC).CC'\)\(= \left( {9 + 12 + 15} \right).10 = 360\;(c{m^2})\) Diện tích mặt đáy hình lăng trụ là: \(S = \displaystyle {1 \over 2}.9.12 = 54\;(c{m^2})\) Diện tích toàn phần hình lăng trụ là: \({S_{TP}} ={S_{xq}}+2.S= 360 + 2.54 = 468\;(c{m^2})\) Thể tích của hình lăng trụ là: \(V = S.h = 54.10 = 540\;(c{m^3})\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
