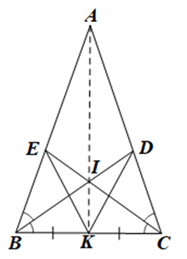
Giải Bài 81 trang 92 sách bài tập toán 7 - Cánh diềuCho tam giác ABC cân tại A có K là trung điểm của đoạn BC. Hai đường phân giác BD và CE cắt nhau tại I. Chứng minh: Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC cân tại A có K là trung điểm của đoạn BC. Hai đường phân giác BD và CE cắt nhau tại I. Chứng minh: a) I cách đều ba cạnh của tam giác ABC; b) KI là tia phân giác của góc EKD. Phương pháp giải - Xem chi tiết - Chứng minh: giao điểm I của hai đường phân giác BD và CE cũng thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC nên I cách đều ba cạnh AB, BC, AC. - Chứng minh: A, I, K thẳng hàng. KA là đường phân giác của góc EKD. Suy ra: KI là tia phân giác của góc EKD. Lời giải chi tiết a) Vì ba đường phân giác của tam giác ABC cùng đi qua một điểm nên giao điểm I của hai đường phân giác BD và CE cũng thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC. Suy ra I cách đều ba cạnh AB, BC, AC. Vậy I cách đều ba cạnh của tam giác ABC. b) • Vì BD là tia phân giác của góc ABC nên \(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC}\). Vì CE là tia phân giác của góc ACB nên \(\widehat {ACE} = \widehat {ECB} = \frac{1}{2}\widehat {ACB}\). Mà \(\widehat {ABC} = \widehat {ACB}\) (do tam giác ABC cân tại A). Suy ra \(\widehat {ABD} = \widehat {DBC} = \widehat {ACE} = \widehat {ECB}\) • Xét ∆ABD và ∆ACE có: \(\widehat {BAC}\) chung AB = AC (do tam giác ABC cân tại A), \(\widehat {ABD} = \widehat {ACE}\) (chứng minh trên). Do đó ∆ABD = ∆ACE (g.c.g). Suy ra AD = AE (hai cạnh tương ứng). • Xét ∆ABK và ∆ACK có: AB = AC (chứng minh trên), AK là cạnh chung, BK = CK (do K là trung điểm của BC). Do đó ∆ABK = ∆ACK (c.c.c). Suy ra \(\widehat {BAK} = \widehat {CAK}\) (hai góc tương ứng). Hay \(\widehat {EAK} = \widehat {DAK}\). • Xét ∆AEK và ∆ADK có: AE = AD (chứng minh trên), \(\widehat {EAK} = \widehat {DAK}\) (chứng minh trên), AK là cạnh chung. Do đó ∆AEK = ∆ADK (c.g.c) Suy ra \(\widehat {AKE} = \widehat {AKD}\) (hai góc tương ứng) Nên KA là đường phân giác của góc EKD. Mặt khác do \(\widehat {BAK} = \widehat {CAK}\) nên AK là tia phân giác của góc BAC. Mà theo câu a, I thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC Nên AI cũng là đường phân giác của góc BAC. Do vậy, ba điểm A, I, K thẳng hàng. Khi đó KI cũng là đường phân giác của góc EKD. Vậy KI là tia phân giác của góc EKD.
|