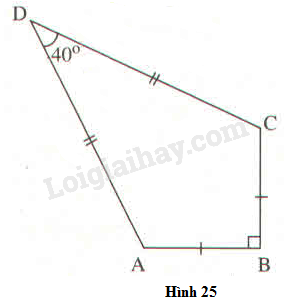
Bài 71 trang 116 SBT toán 9 tập 1

Đề bài

Một chiếc diều \(ABCD\) có \(AB = BC, AD = DC.\) Biết \(AB = 12cm,\widehat {ADC} = 40^\circ \)

\(\widehat {ABC} = 90^\circ \) (h.25)  

  

Hãy tính:

a) Chiều dài cạnh \(AD;\)

b) Diện tích của chiếc diều.

Lời giải chi tiết

 

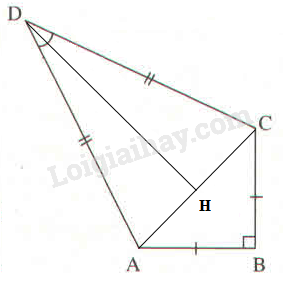
a) Nối \(AC\) và kẻ \(DH \bot AC\)

Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABC,\) ta có:

\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} \cr 
& = {12^2} + {12^2} = 144 + 144 = 288 \cr} \)

Suy ra: \(AC = 12\sqrt 2 \,(cm)\)

Ta có: tam giác \(ACD\) cân tại \(D\) mà \(DH \bot AC\) nên DH cũng là đường trung tuyến và đường phân giác của tam giác. 

Suy ra: \(\displaystyle  HA = HC = {{AC} \over 2} = 6\sqrt 2 \,(cm)\)

Và \(\displaystyle  \widehat {ADH} = {1 \over 2}\widehat {ADC} = 20^\circ \)

Trong tam giác vuông \(ADH,\) ta có:

\(\eqalign{
& {\rm{AD = }}\displaystyle {{AH} \over {\sin \widehat {ADH}}} \cr 
& = {{6\sqrt 2 } \over {\sin 20^\circ }} \approx 24,809\,(cm) \cr} \)

b) Ta có:

\(\displaystyle  {S_{ABC}} = {1 \over 2}.AB.BC \)\(\displaystyle = {1 \over 2}.12.12 = 72\,(cm^2)\)

Trong tam giác vuông \(ADH,\) ta có:

\(\eqalign{
& DH = AH.\cot \widehat {ADH} \cr 
& = 6\sqrt 2 .\cot 20^\circ \approx 23,313\,(cm) \cr} \)

Mặt khác:

\(\eqalign{
& {S_{ADC}} = {1 \over 2}.DH.AC \cr 
& \approx {1 \over 2}.23,313.12\sqrt 2 = 197,817 cm^2 \cr} \) 

Vậy diện tích diều là:

\(\eqalign{
& S= {S_{ABC}} + {S_{ADC}} \cr 
& = 72 + 197,817 = 269,817 cm^2.\cr} \) 

HocTot.Nam.Name.Vn