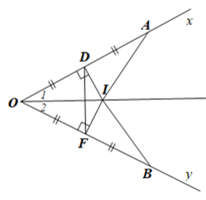
Giải Bài 69 trang 88 sách bài tập toán 7 - Cánh diều

Đề bài

Cho góc xOy nhọn. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của đoạn thẳng OA và đường trung trực của đoạn thẳng OB cắt nhau tại I. Chứng minh:

a) OI là tia phân giác của góc xOy;

b) OI là đường trung trực của đoạn thẳng AB.

Lời giải chi tiết

Gọi D và F lần lượt là trung điểm của OA và OB.

a) Ta có:

DI là đường trung trực của OA nên IO = IA.

FI là đường trung trực của OB nên IO = IB.

Suy ra IO = IA = IB

Xét ∆OIA và ∆OIB có:

OA = OB (giả thiết),

OI là cạnh chung,

IA = IB (chứng minh trên)

Do đó ∆OIA = ∆OIB (c.c.c).

Suy ra \({\hat O_1} = {\hat O_2}\) (hai góc tương ứng).

Do đó OI là tia phân giác của góc xOy.

Vậy OI là tia phân giác của góc xOy.

b) Theo giả thiết OA = OB suy ra O cách đều A và B.

Do đó O nằm trên đường trung trực của đoạn thẳng AB.

Theo chứng minh ở câu a: IA = IB suy ra I cách đều A và B.

Do đó I nằm trên đường trung trực của đoạn thẳng AB.

Vậy OI là đường trung trực của đoạn thẳng AB.