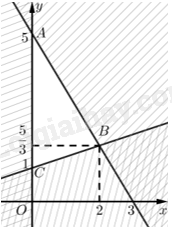
Giải bài 6 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạoGiải bài toán quy hoạch tuyến tính: F=40x+15y→max với ràng buộc \left\{ \begin{array}{l}5{\rm{x}} + 3y \le 15\\x + 3 \le 3y\\x \ge 0\end{array} \right. Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Giải bài toán quy hoạch tuyến tính: F = 40x + 15y \to \max ,\min với ràng buộc \left\{ \begin{array}{l}5{\rm{x}} + 3y \le 15\\x + 3 \le 3y\\x \ge 0\end{array} \right. Phương pháp giải - Xem chi tiết Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ Oxy. Bước 2: Tính giá trị của biểu thức F tại các đỉnh của {\Omega }. Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của F trên {\Omega }. Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số a và b không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của F trên {\Omega }. Lời giải chi tiết Viết lại ràng buộc: \left\{ \begin{array}{l}5{\rm{x}} + 3y \le 15\\x - 3y \le - 3\\x \ge 0\end{array} \right. Tập phương án {\Omega } là miền tam giác ABC.
Ta có: A\left( {0;5} \right),C\left( {0;1} \right). Toạ độ B là nghiệm của hệ \left\{ \begin{array}{l}5{\rm{x}} + 3y \le 15\\x - 3y \le - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \frac{5}{3}\end{array} \right.. Vậy B\left( {2;\frac{5}{3}} \right) Giá trị của biểu thức F tại các đỉnh của {\Omega }: F\left( {0;5} \right) = 75,F\left( {2;\frac{5}{3}} \right) = 105,F\left( {0;1} \right) = 15. Do đó: \mathop {\max }\limits_{\Omega } F = F\left( {2;\frac{5}{3}} \right) = 105;\mathop {\min }\limits_{\Omega } F = F\left( {0;1} \right) = 15.  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
