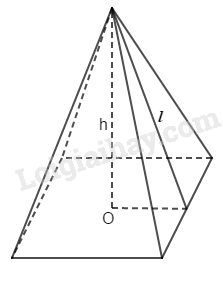
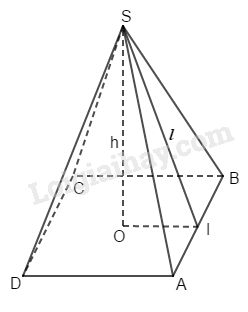
Bài 59 trang 150 SBT toán 8 tập 2

Đề bài

Cho hình chóp tứ giác đều (h.146). Xem hình và điền số thích hợp vào các ô còn trống ở bảng sau:

Chiều cao \((h)\)	8	15
Trung đoạn \((l)\)	10		15
Cạnh đáy		16	12	10
\({S_{xq}}\)				120

Lời giải chi tiết

Gọi độ dài cạnh đáy là \(a.\) Khi đó, \(a=2.OI.\)

Áp dụng định lí Pytago vào tam giác vuông \(SOI\), ta có:

\(\begin{array}{l}
S{I^2} = S{O^2} + O{I^2}\\\Rightarrow SI = \sqrt {O{I^2} + S{O^2}}=l\\
\Rightarrow OI = \sqrt {S{I^2} - S{O^2}}= \sqrt {{l^2} - {h^2}}\\
\Rightarrow SO = \sqrt {S{I^2} - O{I^2}}=h 
\end{array}\)

Diện tích xung quanh hình chóp đều là:

\({S_{xq}} = 2.a.l\)

+) Nếu \(h=8;\;l=10\) thì ta có:

\(OI = \sqrt {{{10}^2} - {8^2}}  = 6\) do đó \(a = 2OI = 2.6 = 12\)

\({S_{xq}} = 2.10.12 = 240\)

+) Nếu \(h=15;\;a=16\) thì ta có:

\(OI=16:2=8\)

\( \Rightarrow l = \sqrt {{{15}^2} + {8^2}}  = 17\)

\({S_{xq}} = 2.17.16 = 544\)

+) Nếu \(l=15;\;a=12\) thì ta có:

\(OI=12:2=6\)

\( \Rightarrow h = \sqrt {{{15}^2} - {6^2}}  = \sqrt {189} \)

\({S_{xq}} = 2.15.12 = 360\)

+) Nếu \(a=10;\;S_{xq}=120\) thì ta có:

\( \Rightarrow l = \dfrac{{{S_{xq}}}}{{2a}} = \dfrac{{120}}{{2.10}} = 6\)

\(OI=10:2=5\)

\( \Rightarrow h = \sqrt {{6^2} - {5^2}}  = \sqrt {11} \)

Ta điền vào bảng như sau:

Chiều cao \((h)\)	8	15	\(\sqrt {189} \)	\(\sqrt {11} \)
Trung đoạn \((l)\)	10	17	15	6
Cạnh đáy \((a)\)	12	16	12	10
\({S_{xq}}\)	240	544	360	120

HocTot.Nam.Name.Vn