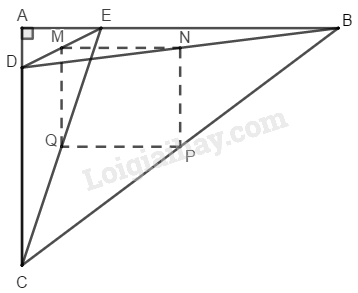
Bài 5.3 phần bài tập bổ sung trang 163 SBT toán 8 tập 1

Đề bài

Cho tam giác vuông \(ABC,\) có hai cạnh góc vuông là \(AC = 6\,cm\) và \(AB = 8\,cm.\) Trên cạnh \(AC\) lấy điểm \(D\) sao cho \(CD = 5\,cm.\) Trên cạnh \(AB\) lấy điểm \(E\) sao cho \(EB = 5\,cm.\) Gọi \(M,\, N,\, P,\, Q\) tương ứng là trung điểm của các đoạn thẳng \(DE,\, DB,\, BC\) và \(CE.\) Tính diện tích của tứ giác \(MNPQ.\)

Lời giải chi tiết

+) Trong \(∆ EDC\) ta có:

\(M\) là trung điểm của \(ED\)

\(Q\) là trung điểm của \(EC\)

nên \(MQ\) là đường trung bình của \(∆ EDC\)

\(⇒ MQ = \dfrac{1}{2}CD = 2,5\, (cm)\) và \(MQ // CD\)

+) Trong \(∆ BDC\) ta có:

\(N\) là trung điểm của \(BD\)

\(P\) là trung điểm của \(BC\)

nên \(NP\) là đường trung bình của \(∆ BDC\)

\(⇒ NP = \dfrac{1}{2}CD = 2,5\, (cm)\)

+) Trong \(∆ DEB\) ta có:

\(M\) là trung điểm của \(DE\)

\(N\) là trung điểm của \(DB\)

nên \(MN\) là đường trung bình của \(∆ DEB\)

\(⇒ MN = \dfrac{1}{2}BE = 2,5\, (cm)\) và \(MN // BE\)

+) Trong \(∆ CEB\) ta có:

\(Q\) là trung điểm của \(CE\)

\(P\) là trung điểm của \(CB\)

nên \(QP\) là đường trung bình của \(∆ CEB\)

\(⇒ QP =  \dfrac{1}{2}BE = 2,5\, (cm)\)

Suy ra: \(MN = NP = PQ = QM \) (1)

\(MQ // CD\) hay \(MQ // AC\)

\(AC ⊥ AB\) (do tam giác ABC vuông tại A)

\(⇒ MQ ⊥ AB\)

Lại có: \(MN // BE\) hay \(MN // AB\)

Suy ra: \(MQ ⊥ MN\) hay \(\widehat {QMN} = 90^\circ \) (2)

Từ (1) và (2) suy ra tứ giác \(MNPQ\) là hình vuông

\({S_{MNPQ}} = M{N^2} = {\left( {2,5} \right)^2} = 6,25\) \((c{m^2})\)

HocTot.Nam.Name.Vn