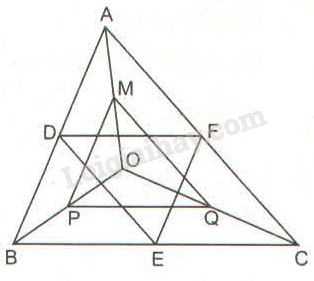
Bài 5.2 phần bài tập bổ sung trang 91 SBT toán 8 tập 2

Đề bài

Cho tam giác ba góc nhọn $ABC$ và một điểm $O$ bất kì trong tam giác đó.

Ba điểm $D, E, F$ theo thứ tự là trung điểm các cạnh $AB, BC$ và $CA.$ Ba điểm $M, P, Q$ theo thứ tự là trung điểm của các đoạn thẳng $OA, OB$ và $OC.$

a) Các tam giác $DEF$ và $MPQ$ có đồng dạng với nhau không? Vì sao? Tỉ số đồng dạng bằng bao nhiêu?

Hãy sắp xếp các đỉnh tương ứng nếu hai tam giác đó đồng dạng.

b) Khi nào thì lục giác $DPEQFM$ có tất cả các cạnh bằng nhau? Hãy vẽ hình trong trường hợp đó.

Lời giải chi tiết

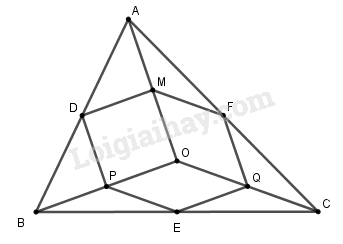
a) Theo giả thiết $D, E, F$ lần lượt là trung điểm các cạnh $AB, BC$ và $CA$ nên $DE, EF, FD$ là các đường trung bình của tam giác $ABC.$ Do đó, ta có:

$\displaystyle DE = {1 \over 2}AC,EF = {1 \over 2}AB,$ $\displaystyle FD = {1 \over 2}BC$ (1) (tính chất đường trung bình)

Mặt khác, $M$ là trung điểm của $OA,$ $P$ là trung điểm của $OB,$ $Q$ là trung điểm của $OC,$ xét các tam giác $OAB, OBC, OCA$ có $MP, PQ, MQ$ lần lượt là đường trung bình nên ta có:

$\displaystyle MP = {1 \over 2}AB,PQ = {1 \over 2}BC,$ $\displaystyle QM = {1 \over 2}AC$ (2) (tính chất đường trung bình)

Từ (1) và (2), ta suy ra:

$DE = QM, EF = MP, FD = PQ.$

Do đó: $\displaystyle {{DE} \over {QM}} = {{EF} \over {MP}} = {{FD} \over {PQ}} = 1$

Vậy $∆ DEF$ đồng dạng $∆ QMP$ theo tỉ số đồng dạng $k = 1$, trong đó $D, E, F$ lần lượt tương ứng với các đỉnh $Q, M, P.$

b) Lục giác $DPEQFM$ có các cặp cạnh đối bằng nhau từng đôi một:

$DP = QF$ (vì cùng bằng $\displaystyle {1 \over 2}OA);$

$PE = MF$ (vì cùng bằng  $\displaystyle {1 \over 2}OC)$

$EQ = MD$ (vì cùng bằng $\displaystyle {1 \over 2}OB)$

Lục giác $DPEQFM$ có $6$ cạnh bằng nhau chỉ khi $DP = PE = EQ.$

Muốn vậy, ta phải có $OA = OB = OC$, khi đó $O$ là điểm cách đều ba điểm $A, B, C$.

Vậy $O$ là giao điểm của ba đường trung trực tam giác $ABC.$

HocTot.Nam.Name.Vn