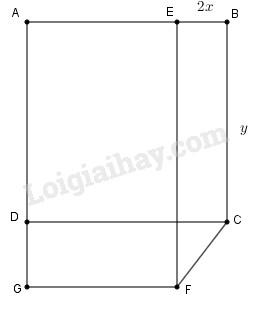
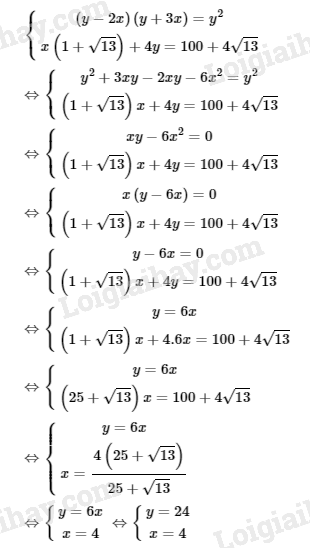Bài 50 trang 15 SBT toán 9 tập 2

Đề bài

Cho hình vuông \(ABCD\) cạnh \(y (cm)\). Điểm \(E\) thuộc cạnh \(AB\). Điểm \(G\) thuộc tia \(AD\) sao cho \(AG = AD +\displaystyle  {3 \over 2}EB.\) Dựng hình chữ nhật \(GAEF.\)

Đặt \(EB = 2x (cm)\). Tính \(x\) và \(y\) để diện tích của hình chữ nhật bằng diện tích hình vuông và ngũ giác \(ABCFG\) có chu vi bằng \(100 + 4\sqrt {13}(cm) \)

Lời giải chi tiết

Theo giả thiết ta có: \(EB = 2x (cm)\) 

Điều kiện: \(y > 2x > 0\)

\(AE = AB – EB = y – 2x (cm)\)

\(AG = AD + DG\)\( = y +\displaystyle {3 \over 2}EB \\ = y + \displaystyle{3 \over 2}.2x = y + 3x(cm)\)

\( \Rightarrow DG = 3x\)

Diện tích hình chữ nhật \(GAEF\) bằng diện tích hình vuông  \(ABCD\) nên ta có phương trình:

\(\left( {y - 2x} \right)\left( {y + 3x} \right) = {y^2}\)

Mặt khác theo định lí Pitago ta có:

\(FC = \sqrt {E{B^2} + D{G^2}}  \\ = \sqrt {4{x^2} + 9{x^2}}  = x\sqrt {13} (cm)\)

Chu vi của ngũ giác \(ABCFG\) bằng: 

\(\eqalign{
& AB + BC + CF + FG + GA \cr 
& = y + y + x\sqrt {13} + y - 2x + 3x + y \cr 
& = x\left( {1 + \sqrt {13} } \right) + 4y \cr} \)

Chu vi ngũ giác \(ABCFG\) bằng \(100 + 4\sqrt {13}  (cm)\) nên ta có phương trình:

\(x\left( {1 + \sqrt {13} } \right) + 4y = 100 + 4\sqrt {13} \)

Ta có hệ phương trình:

Giá trị \(x = 4\) và \(y = 24\) thỏa mãn điều kiện bài toán.

Vậy \(x = 4 (cm); y = 24 (cm).\)

HocTot.Nam.Name.Vn