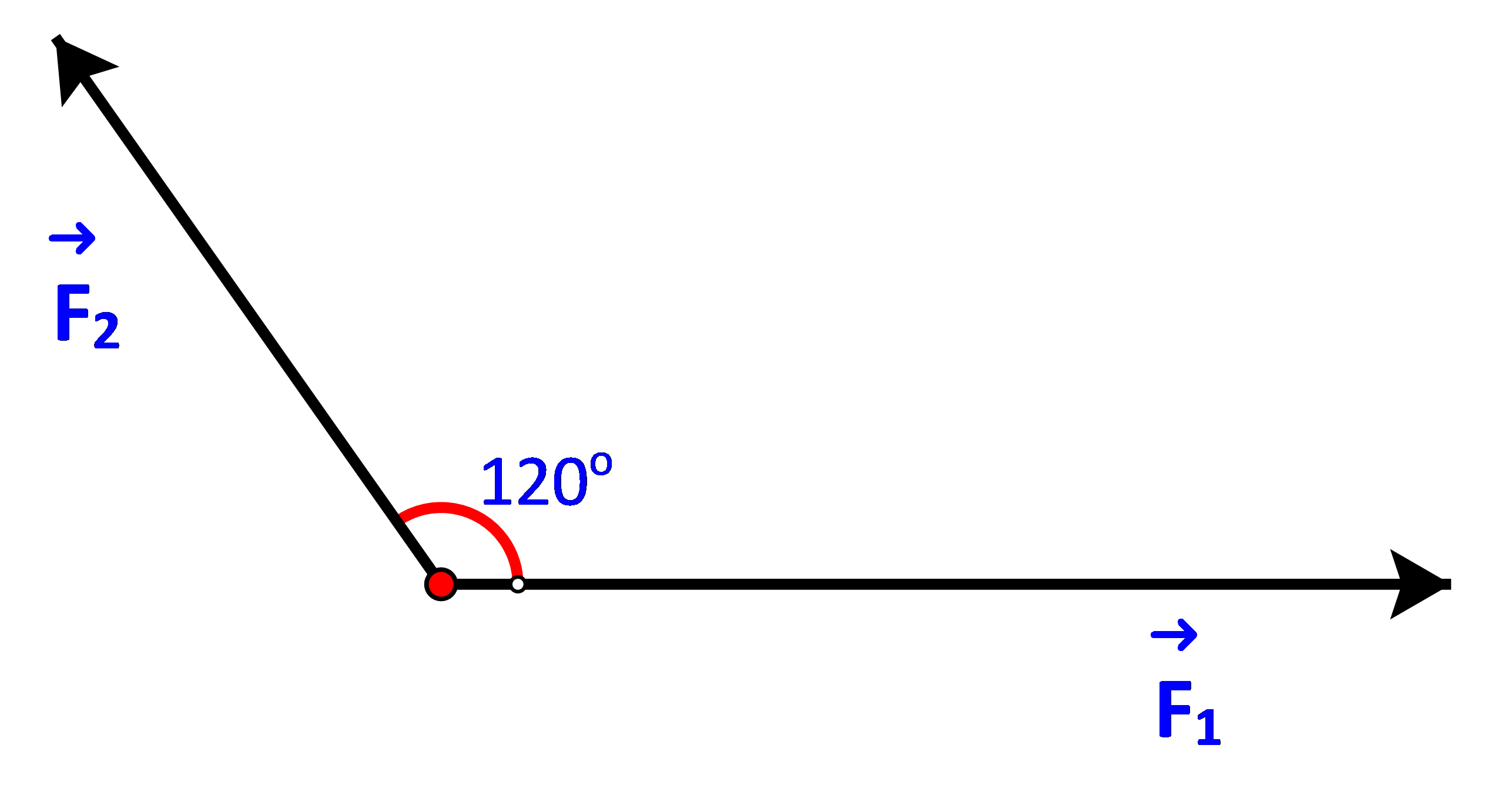
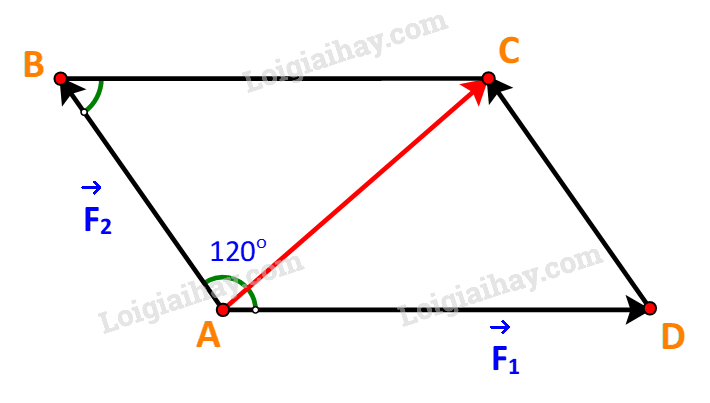
Giải bài 4.9 trang 54 SGK Toán 10 tập 1 – Kết nối tri thức

Đề bài

Hình 4.19 biểu diễn hai lực $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}}$ cùng tác động lên một vật, cho $\left| {\overrightarrow {{F_1}} } \right| = 3\;N,\;\left| {\overrightarrow {{F_2}} } \right| = 2\;N.$ Tính độ lớn của hợp lực $\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}$.

Lời giải chi tiết

Dựng hình bình hành ABCD với hai cạnh là hai vectơ $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}}$ như hình vẽ

 

Ta có:

$\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  = \overrightarrow {AD}  + \overrightarrow {AB}  = \overrightarrow {AC}  \Rightarrow \left| {\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC$

Xét $\Delta ABC$ ta có:

$BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.$

$\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}$

Theo định lí cosin ta có:

$\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}$

Vậy $\left| {\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} } \right| = \sqrt {7}$