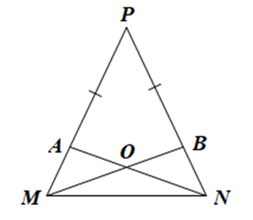
Giải Bài 47 trang 83 sách bài tập toán 7 - Cánh diều

Đề bài

Cho tam giác MNP cân tại P. Lấy điểm A trên cạnh PM, điểm B trên cạnh PN sao cho PA = PB. Gọi O là giao điểm của NA và MB. Chứng minh tam giác OMN là tam giác cân.

Lời giải chi tiết

Vì ∆MNP cân tại P nên ta có:

PM = PN (hai cạnh bên), $\widehat {PMN} = \widehat {PNM}$ (hai góc ở đáy).

Ta có PM = PA + AM, PN = PB + BN.

Mà PM = PN (chứng minh trên), PA = PB (giả thiết).

Suy ra AM = BN.

Xét ∆AMN và ∆BNM có:

AM = BN (chứng minh trên),

MN là cạnh chung,

$\widehat {AMN} = \widehat {BNM}$ (do $\widehat {PMN} = \widehat {PNM}$)

Do đó ∆AMN = ∆BNM (c.g.c).

Suy ra $\widehat {ANM} = \widehat {BMN}$ (hai góc tương ứng).

Hay $\widehat {ONM} = \widehat {OMN}$

Do đó tam giác ONM cân tại O.

Vậy tam giác OMN là tam giác cân tại O.