Bài 44 trang 107 SBT toán 9 tập 2

Đề bài

Vẽ hình vuông \(ABCD\) tâm \(O\) rồi vẽ tam giác đều có một đỉnh là \(A\) và nhận \(O\) làm tâm. Nêu cách vẽ.

Lời giải chi tiết

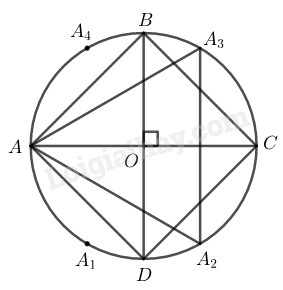
Cách vẽ:  

− Vẽ đường tròn \((O; R)\)

− Kẻ \(2\) đường kính \(AC ⊥ BD\)

− Nối \(AB, BC, CD, DA\) ta được tứ giác \(ABCD\) là hình vuông nội tiếp trong đường tròn \((O; R)\)

− Từ \(A\) đặt liên tiếp các cung bằng nhau có dây tương ứng bằng bán kính \(R\) là: 

\(\overparen{{A}{A_1}},\) \(\overparen{{A_1}{A_2}},\) \(\overparen{{A_2}{C}},\) \(\overparen{{C}{A_3}},\) \(\overparen{{A_3}{A_4}}\)

Nối \({{A}{A_2}},\)\({{A_2}{A_3}},\)\({{A_3}{A}},\) ta có \(∆{{A}{A_2}{A_3}},\) là tam giác đều nhận \(O\) làm tâm.

Chứng minh:

Vì các cung \(\overparen{{A}{A_1}},\) \(\overparen{{A_1}{A_2}},\) \(\overparen{{A_2}{C}},\) \(\overparen{{C}{A_3}},\) \(\overparen{{A_3}{A_4}}\) bằng nhau nên ta có:

\(\overparen{{A}{A_2}}\)\(=\overparen{{A_2}{A_3}}\)\(=\overparen{{A_3}{A}}\)

Suy ra \(AA_2=A_2A_3=A_3A\) nên tam giác \({{A}{A_2}{A_3}}\) là tam giác đều

Theo cách vẽ ta có \(O\) là tâm đường tròn ngoại tiếp tam giác \({{A}{A_2}{A_3}}\)

Vậy tam giác \({{A}{A_2}{A_3}}\) thỏa mãn đề bài. 

HocTot.Nam.Name.Vn