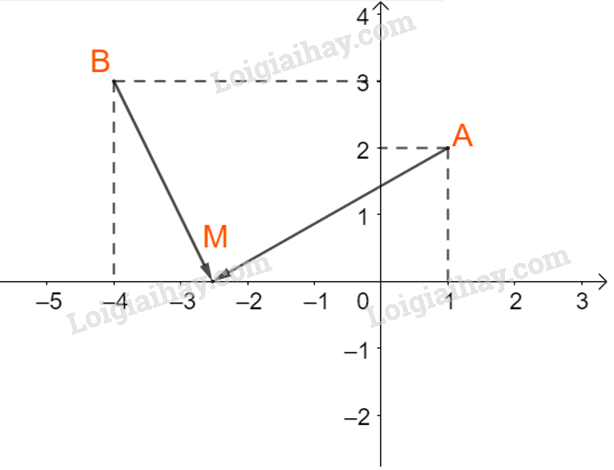
Giải bài 4.23 trang 70 SGK Toán 10 – Kết nối tri thứcTrong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2), B(-4; 3). Gọi M (t; 0) là một điểm thuộc trục hoành. a) Tính AM.BM theo t. b) Tính t để góc AMB = 90^o Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2), B(-4; 3). Gọi M (t; 0) là một điểm thuộc trục hoành. a) Tính \(\overrightarrow {AM} .\overrightarrow {BM} \) theo t. b) Tính t để \(\widehat {AMB} = {90^o}\) Phương pháp giải - Xem chi tiết +) Nếu vecto \(\overrightarrow {AM} (x;y)\) và \(\overrightarrow {BM} (a;b)\) thì \(\overrightarrow {AM} .\overrightarrow {BM} = xa + yb\) +) \(\widehat {AMB} = {90^o} \Leftrightarrow AM \bot BM\) Lời giải chi tiết
a) Ta có: A (1; 2), B(-4; 3) và M (t; 0). \(\begin{array}{l} b) Để \(\widehat {AMB} = {90^o}\) hay \(AM \bot BM\) thì \(\overrightarrow {AM} .\overrightarrow {BM} = 0\) \(\begin{array}{l} \Leftrightarrow {t^2} + 3t + 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = - 2\end{array} \right.\end{array}\) Vậy t = -1 hoặc t = -2 thì \(\widehat {AMB} = {90^o}\).
|